Jette Randløv
Svaret på sidste nummers tretraeder-pyramideopgave er ikke 7 sider - som man kunne forvente - men 5. To af pyramidens sider og to af tretraederets sider ligger nemlig i samme plan.
Det indses nok nemmest ved at lave en model i papir og bruge nogle
simple geometriske argumenter. Det kan også klares uden en figur. Hvis
vi placerer pyramiden i et koordinatsystem med hjørnerne af basen i
hjørnerne af enhedkvadratet, får vi, at toppen må ligge i
. (De to første
koordinater indses med et symmetriargumnet og den sidste med
Pythagoras sætning.) Tetraederen påklæbes nu i pyramidetrekanten ud
af x-aksen. Koordinaterne for det hjørne af tetraederens, som ikke
berører pyramiden, må være 
(atter lidt symmetri og Pythagoras). Vi ser
nu på de to trekanter, som vender væk fra y-aksen. Der gælder nu, at
pyramidens trekant og tetraederens trekant ligger i samme plan, hvis
og kun hvis linjen fra pyramidens top til (1,0,0) og linjen fra
(0,0,0) og det hjørne af tetraederen, som ikke berører pyramiden,
skærer hinanden. (Den første linje ligger der, hvor pyramiden og tretraederet
rør hinanden.) Den første linje kan skrives som
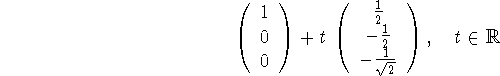
Og den anden linje som
Det ses at disse to linjer skærer hinanden (med 
, 
).