Carsten Svaneborg
De to forgående artikler
har handlet om at løse
optimeringsproblemer ved hjælp af algoritmer, hvor en funktion er
kendt som funktion af en mængde af kontinuerte og/eller diskrete
variable, men hvor de afledte af funktionen ikke er kendt eller ikke
er defineret. I det følgende vil vi antage, at der er et kontinuum af
ukendte variable givet ved en differentiabel funktion f(x), samt en
funktional. Vi leder efter den funktion, der minimerer/maksimerer
funktionalen.
Der er mange eksempler på problemer, der kan formuleres på denne måde, for eksempel Fermats princip, der siger, at lyset fra en lyskilde i punktet A, der bliver detekteret i B, vil følge den kurve fra A til B, hvor lyset når hurtigst (eller langsomst) frem, og af Fermats Princip følger geometrisk optik. Af samme skuffe er en geodæt, der er den korteste rute mellem to punkter. En klassiker er brachistochronproblemet (gr. kortest tid), der var det første variationsproblem og blev stillet af Jakob Bernoulli i 1696. Populært formuleret lyder det som følger: Hvilken profil skal en bakke have, for at en bold, der starter fra toppen, hurtigst vil nå bunden (når man ser bort fra rotation og friktion)?
Givet et linært normeret rum 
af passende differentiable
funktioner (her 
) og en funktional 
, kan partiel differentation generaliseres til
Hvis ovenstående eksisterer for alle 
, kaldes
udtrykket for gâteaux-variationen af funktionalen; 
er
mængen af funktioner, man varierer over, og antages at være en lineær
delmængde af , idet man oftest vil have bestemte kriterier
for h. I det følgende er 
, svarende til at endepunkterne i variationen
fastholdes.
Et interessant eksempel (folk, der har haft analytisk mekanik, vil
genkende eksemplet og notationen): Hvis 
, hvor L(x,y,z) er en differentiabel
funktion, og 
, så er gâteaux-variationen:
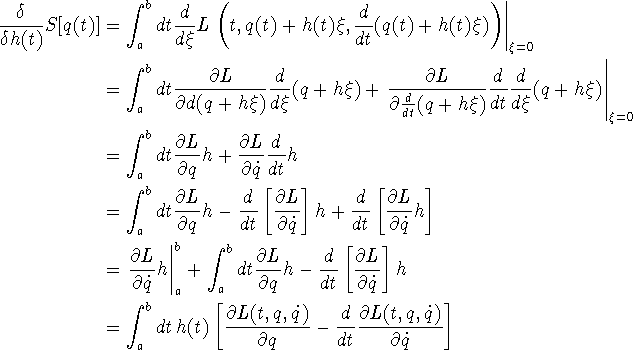
Fra den 3. til den 4. ligning er udtrykket for differention af produktfunktioner brugt, og i den sidste ligning er brugt, at grænseledet forsvinder da h(a)=h(b)=0.
For en funktion 
, der er et ekstremum (relativt til
og normen på dette rum) for funktionalen I[f], gælder
denne ligning kaldes Euler-Lagrange (EL) ligningen, og nu er det
praktisk at variationsregningens fundementallemma giver (for 
), at
dvs., at man kan slippe af med h(t) og integralet på letteste vis.
Med funktionalen fra eksemplet indsat, giver EL og lemmaet følgende:
Denne ligning kaldes også for Euler-Lagrange-ligningen for funktionalen S[q(t)].
Ligningen kan umiddelbart generaliseres til det tilfælde, hvor
, dvs., funktionalen
er afhængig af N funktioner i stedet
for kun en funktion, og resultatet er N EL-ligninger, med samme
form som den forrige EL-ligning, bare krydret med j'er:
Eksemplet er ikke valgt tilfældigt. Beskrives et fysisk system ved N
koordinater 
i et vilkårligt koordinatsystem (fx sphæriske
koordinater), og identificeres 
(Lagrange funktionen) med forskellen i kinetisk og potentiel
energi (til tiden t i punktet ) udtrykt i det valgte
koordinatsystem, da kaldes 
for aktion-funktionalen (og det er
ikke tilfældigt, at den har samme dimension som 
(energi gange
tid, red.)), og sættet af Euler-Lagrange-ligningerne er en
generalisering af Newtons bevægelsesligning til det valgte
koordinatsystem.
Hvis et koordinatsystem har en metrisk tensor 
, dvs.,
at pythagoras's læresætning i et punkt 
for et differentielt
skridt 
er 
, da er
Lagrange funktionen for en fri partikel 
, og 
, men
funktionalen 
har
samme extrema, da EL-ligningen vil blive multipliceret med 
(hvis T>0), som derfor kan divideres ud.
Men 
er længden af den kurve, partiklen vil følge.
Extrema for denne funktional er faktisk geodæter, dvs., at en fri
partikel vil følge geodæter. Dette udsagn er korrekt både i klassisk
mekanik såvel som generel relativitetsteori, og kan fx observeres ved
en 
afbøjning af lys fra stjerner set tæt ved solens
overflade.
For en partikel beskrevet af 1 (kartesisk) dimension (dvs.
q(t)=x(t)), og i et potential U(x) er 
, indsat i EL-ligningen:
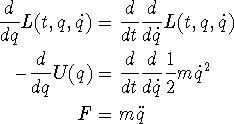
Dvs., EL-ligningerne reducerer til Newtons anden lov i kartesiske koordinater. Det er ofte praktisk at kunne anvende et smart koordinatsystem, i stedet for kartesiske koordinater. Fx et pendul kræver 2 koordinater, og i kartesiske koordinater er Newton kedelig at løse, men i polære koordinater er problemet trivielt.
Nu er de forgående eksempler mekaniske, men EL-ligningen gælder for
enhver funktional, der kun indeholder 
og 
, og det er
let at generalisere EL til højere afledede. For problemerne nævnt i
indledningen er (i 2D kartesiske koordinater) Fermats princip
,
hvor T er passagetiden (lyshastigheden c=1) og n(x,y) er
brydningsindekset, og både geodæt- og brachistochronfunktionalerne er
specialtilfælde med n(x,y(x))=1 hhv. 
.
Der findes mange andre problemer, der kan formuleres som variationsproblemer udover al klassisk mekanik (inkl. Maxwells ligninger og generel relativitetsteori). En anden gruppe er kontrolproblemer, hvor man ønsker en kontrolfunktion, der maksimerer ens kontrol over et kendt system, fx en laserpulsform, der selektivt eksiterer atomer til en ønsket tilstand, eller bryder en bestemt binding i et molekyle. Et andet og meget visuelt eksempel er sæbebobler på en ståltrådsfigur (hvor eksperimentet nok er mere gennemsigtigt end matematikken) hvor overfladeenergien skal minimeres, mens volume skal være konstant, og der skal være passende grænsebetingelser svarende til den ståltrådsfigur, som boblen sidder på.