


Foregående: Matematikseminar 1997
Næste: Nyt fra Centralmatematisk Fagråd
Op: FAMØS september 1997
Henrik Chr. Grove
I sidste nummer havde vi et "`bevis"' for at  , opgaven var så at
finde fejlen. Før jeg røber løsningen, så lad mig lige fortælle at opgaven
stammer fra internetnyhedsgruppen
, opgaven var så at
finde fejlen. Før jeg røber løsningen, så lad mig lige fortælle at opgaven
stammer fra internetnyhedsgruppen sci.math, hvor den blev postet af en
amerikansk gymnasielærer, der havde set nogle af hans lave ``beviset''. Hvis
der (mod forventning) skulle være nogen der ikke har fundet fejlen, så den
mellem linie 6 og 7, indholdet af parentesen på venstre side er positivt, mens
indholdet på højre side er negativt, hvorfor man selvfølgelig ikke kan tage
kvadratroden på begge side, som det blev gjort i udregningerne i opgaven.
Det sjove i opgaven ligger dog et helt andet sted. Mellem linie 2 og 3 ganges
der nemlig med 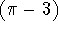 , men hvis konklusionen var rigtig så var
, men hvis konklusionen var rigtig så var 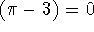 , og man må som bekendt ikke gange med 0. Man kan overveje om dette i sig
selv er en fejl, men hvis vi udnytter, hvad vi ved om
, og man må som bekendt ikke gange med 0. Man kan overveje om dette i sig
selv er en fejl, men hvis vi udnytter, hvad vi ved om  kan det ikke være
en fejl. Dette afslører samtidigt, hvad det er, der er gået galt for de
stakkels amerikanske gymnasieelever. De har glemt, at definitionen på
kan det ikke være
en fejl. Dette afslører samtidigt, hvad det er, der er gået galt for de
stakkels amerikanske gymnasieelever. De har glemt, at definitionen på  giver os visse egenskaber ved dette tal og, at man må kræve, at mindst en af
disse egenskaber anvendes ved et bevis, der handler om dette tal. I stedet har
de ladet sig forlede af, at
giver os visse egenskaber ved dette tal og, at man må kræve, at mindst en af
disse egenskaber anvendes ved et bevis, der handler om dette tal. I stedet har
de ladet sig forlede af, at  har en betegnelsen der for det til at ligne
en variabel, og så brugt det som en sådan.
har en betegnelsen der for det til at ligne
en variabel, og så brugt det som en sådan.
Lars Winther Christensen havde desuden ``gemt'' en lille opgave i sin side 9
sætning (FAMØS maj 1997), nemlig et lille kryptogram. Ved at lave statistik på bogstaverne i
kryptogrammet, finder man rimelig nemt ud, af at den oprindelige tekst var:
"`Teksten her er et simpelt eksempel på en monoalfabetisk substitution STOP
Trods de få karakterer er der god overensstemmelse med den danske
sprogstatisrik "', hvor de store bogstaver er min "`opfindelse"'.



Foregående: Matematikseminar 1997
Næste: Nyt fra Centralmatematisk Fagråd
Op: FAMØS september 1997
famos@math.ku.dk
Wed Oct 1 21:23:03 CEST 1997