Foregående: Reklame Næste: Litteratur Op: FAMØS september 1997

Cantors Mængde og Peanos kurve

Troels Roussau Johansen

Vi skal i det følgende se nærmere på en yderst interessant delmængde af enhedsintervallet [0,1]. Interessen skyldes, at mængden, som vi skal se sidenhen, har nogle ret spøjse egenskaber og dermed kan give anledning til en række modeksempler.

Der lægges ud med en geometrisk konstruktion, men senere vil denne konstruktion få et mere algebraisk tilsnit, da Cantors mængde har en interessant forbindelse til talrepræsentation i 3-talssystemet. Vi vil som en slags kronen på værket runde af med at præsentere en underlig kurve -- Peanos kurve.

Lidt motivation

Det er muligvis velkendt, og under alle omstændigheder ikke så svært at bevise, at der gælder følgende

Vi har således styr på åbne mængder i , men så må den mest generelle afsluttede delmængde af kunne fås ved fra at fjerne en tællelig, disjunkt klasse af åbne intervaller. Det lyder umiddelbart helt uskyldigt...

Konstruktion af Cantors mængde

Vi starter med det afsluttede enhedsinterval . Ud fra dette dannes ved fra at fjerne det åbne interval , dvs. . På samme måde dannes ved fra at fjerne de midterste tredjedele, dvs. .

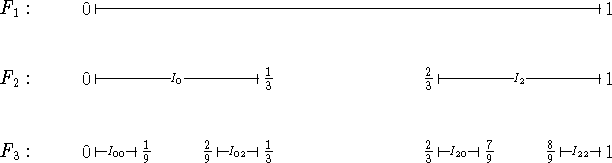
Konstruktionen fortsætter på denne måde, og Cantors mængde er da netop det, der er tilbage, dvs.

Umiddelbare egenskaber ved

Inden vi for alvor går til makronerne er det måske på sin plads at bruge lidt tid på at lære bedre at kende. Først bemærkes, at er kompakt, thi er oplagt begrænset og desuden afsluttet, da jo består af en stor portion afsluttede intervaller. Det var ikke så galt, for kompakte mængder er da pæne? Det er en smagssag, men er ikke så stor, hvad udstrækning angår -- mængden har Lebesgue-mål 0: i n'te skridt fjernes en åben mængde bestående af intervaller af længde , så\

hvoraf sluttes, at . (Denne regneregel er bevist i sidste års 2SS-noter, selvom der ikke blev talt om Lebesguemål. Det er naturligvis også at finde i enhver tekst omhandlende målteori).

Det ville nu være en rimelig formodning at gøre, at ikke indeholder voldsomt mange punkter, men det er langt fra tilfældet, og det er den første ikke-trivielle egenskab ved , vi skal se på:

Mere avancerede egenskaber

Først vil det blive bevist, at og er ækvipotente, og til de læsere, der ikke er bekendt med begrebet `ækvipotens' kommer her et meget lille ``crash-course'':

Begrebet ækvipotens udspringer af ønsket om at kunne sammenligne elementantallet i forskellige mængder indbyrdes. For endelige mængder er det principelt let, da man blot tæller op. For uendelige mængder (for eksempel ) er dette en dårlig idé, så man retter op på situationen med en

Hvis blot f er surjektiv, så er .

Det blev af Cantor bevist, at , og uden bevis nævnes følgende

Bemærk, at selvom dette ser trivielt ud, så er det IKKE tilfældet. Beviset kan for eksempel findes i 3GT-noterne.

Vi kan umiddelbart slutte, at da , så det kunne være sjovt, om vi kunne vise den anden ulighed (idet det bemærkes, at ). Dette vil åbenbart komme ud på at konstruere en surjektiv afbildning , og til dette formål har vi brug for en

Den søgte afbildning fremkommer nu ved at lade g betegne afbildningen

med , hvor er den tilsvarende dualbrøkfremstilling (tænk blot på binære tal). Denne afbildning er oplagt surjektiv, mens den ikke er injektiv (havde det været tilfældet, kunne vi have undværet Bernsteins sætning). Hvad angår den udeblivende injektivitet bemærkes nemlig, at

(idet , hvor , ellers, så , og , hvor , ellers, så etc.). Det lidt overraskende resultat, at , følger nu af Bernstein. Nedenstående omtale overflødiggører iøvrigt helt dette resultat, men det lyder så fint at nævne sætningen...

Når man HAR set g, virker den naturlig nok, men hvordan kommer man på idéen med trialbrøker? Naturligvis fordi vi valgte successivt at tredele [0,1] og smide noget væk. Et vilkårligt punkt kan da karakteres ved successivt at undersøge, hvilke delinteval, x ligger i.

Generelt vil trialbrøkfremstillingen fremstille samme tal som bestemt ved fortsat intervalindsnævring , hvor og er det åbne, begrænsede interval, der fjernes fra for at danne og . Bemærk nemlig, at

(Husk opgave I.5.4 fra Matematik 2AN-noterne).

Hvis vi vil undersøge, om , skal vi således starte med intervalindsnævringen

Da og , er den første del af trialbrøkfremstillingen for . Det er en sjov øvelse at vise, at , , dvs. .

Man kan nu forholdsvis let overbevise sig om, at

Et tal kan snildt have mere end én trialbrøkfremstilling, men hvis blot en af fremstillingerne er 1-fri, er vi tilfredse. Et 1-tal i en entydig fremstilling vil jo betyde, at tallet tilhører et midterinterval, som er fjernet.

Vi vil nu se lidt på et par af 's topologiske egenskaber og lader i det følgende , hvor for alle og er forsynet med den diskrete topologi (alle delmængder defineres til at være åbne). Det følger nu umiddelbart af sætning 7.18 (Tychonoffs Sætning) i 3GT-noterne, at X er kompakt (havde X blot bestået af endeligt mange kopier af havde dette ikke været svært at indse). Det erindres muligvis fra 2AN, at metriske rum besad Hausdorff-egenskaben. Mere generelt har vi følgende

Man kan nu ``hurtigt'' overbevise sig om, at sætning I.6.11 fra 2AN kan generaliseres til

Dette kan vi om lidt benytte til at bevise, at X og er homeomorfe, men først en





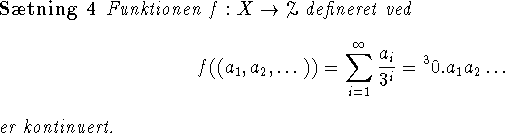
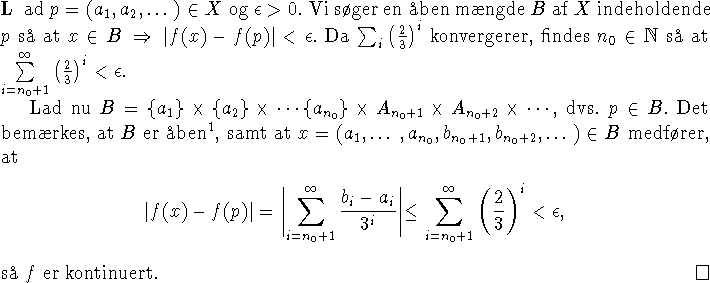
Det kan endvidere bevises, at et kompakt metrisk rum ALTID er et kontinuert billede af .

Peanos kurve

Vi runder af med at benytte den opnåede viden til at konstruere en kontinuert kurve, der går gennem ethvert punkt i enhedskvadratet . Lad os præcisere, hvad vi vil forstå ved en kontinuert kurve:

Lad nu , hvor og , og definér ved . Da er surjektiv. Funktionen er desuden monotont voksende: hvis findes så og dermed er så . Faktisk er også uniformt kontinuert. (Dette er let at vise -- givet findes så\ at . Hvis nu for s,, da stemmer deres trialbrøker overens på de første n pladser. Tilsvarende vil trialbrøkerne for og stemme overens på de første n pladser, så .).

Lad herefter U betegne en af de åbne intervaller, der blev fjernet i konstruktionen af Cantors mængde. Da findes en følge , for alle , så at , og der gælder oplagt, at

Dette viser, at på ethvert fjernet åbent interval antager samme værdi i de to intervalendepunkter. Der findes derfor en entydigt bestemt, monotont voksende funktion , der er kontinuert og desuden stemmer overens med på . h kaldes iøvrigt for Cantor-Lebesgues funktion.

Vi kan nu konstruere Peanos kurve: definer ved at sætte

er da monotont voksende, surjektiv og uniformt kontinuert ( og ligner hinanden, så lad os blot godtage dette), og vi kan udvide til en kontinuert funktion ved at definere til at være lineær på ethvert af de fjernede, åbne intervaller. For eksempel afbildes i linjestykket med endepunkterne og (1,0), idet og . er netop den efterlyste, kontinuerte kurve! Man udtrykker normalt dette ved at sige, at er rumudfyldende. En lidt beskæmmende egenskab er dog, at har uendeligt mange multiple punkter (punkter, der ``rammes'' flere gange). Osgood (1903) har modificeret Peanos kurve, så resultatet er fri for denne defekt.

Epilog

Vi har over de seneste sider leget lidt med Cantors mængde men mulighederne er langt fra udtømte. Den interesserede læser kan læse videre i [3], s. 181-189 for at få en mere håndgribelig beskrivelse af Peanos kurve, eller i [4], s. 145-147 for at stifte bekendtskab med Cantors hullede telt såvel som Cantors tipi.

Foregående: Reklame Næste: Litteratur Op: FAMØS september 1997