Carsten Svaneborg E-post: zqex@@fys.ku.dk
Neurale net har eksisteret ganske længe, lige så længe som der har eksisteret liv med sanser, hvor data fra sanseceller skulle bearbejdes, og bevægelser skulle koordineres, eller liv der har haft reflekser. Siden '42 har vores neurale net (hjernen!) været beskæftiget med opfinde en videnskab ``Neural Computing'', der har beskæftiget sig med at studere modeller af sig selv. Måske vil computere en dag designe nye og bedre computere uden menneskelig indblanding, der kan løse menneskehedens problemer med nutidige computere fx Windows.
Fysiologisk virker hjernen og nervesystemet ved at 
neuroner (decentrale processor enheder), som er forbundet med en
træstruktur af dendritter og axoner (Ind hhv. Ud forbindelser)
gennem synapser. Synapserne spiller rollen af telefoner, hvor
neuronerne kan sende data til hinanden, dendritter er korte
forbindelser, hvor igennem en neuron kan modtager signaler fra
naboneuroner gennem synapseenderne, og axoner sender data til fjernere
neuroner. I gennemsnit forbindes axoner med er par tusinde neuroner,
axoner kan blive over 1 m lange (hvilket der er praktisk, når
hjernen ønsker at bevæge fødderne), signalerne fra/til
neuron og synapse sker vha. natriumioner og en masse kemi.
I 1943 forslog McCulloc og Pitts en simpel model for en (binær)
neuron, lad 
være den j'te neurons output (0=passiv
eller 1=aktiv) til tiden t, så er den i'te neurons output
givet ved 
, hvor
er stepfunktionen, 
er styrken hvormed den
j'te neuron er koblet til den i'te neuron. Denne kan være
både positiv (exiterende) eller negativ (inhibtierende) eller
(ukoblet), og 
er en grænseværdi for den
i'te neuron, modtager neuronen mere indput end grænseværdien
er den aktiv, dvs. at den sender 1 ud på axonerne, er inputtet
mindre en grænseværdien er den passiv (=0).
Ved hjælp af denne simple neuron model viste McCulloc og Pitts, at et net af neuroner med faste koblinger var istand til at udføre de samme grundlæggende logiske operationer, som en digital computer (And,Or etc), dvs. at det var i stand til at gøre det samme, som en logisk computer kan (Universal Computation), men beviset var tungt, og det var ikke let at implementere en given logisk funktion. Neurale net forblev matematik indtil Rosenblatt (1958), inspireret af Hebb's indlæringsmekanism (1949), forslog perceptronen.
Perceptronen er et neuralt netværk med et inputlag og et outputlag, hvor alle inputneuroner er forbundne til alle outputneuroner, hvori koblingerne som er logiske funktioner kan indlæres iterativt (fx på computer), men som Papert og Minsky viste i 1969, kunne kun en delmængde af alle logiske funktioner indlæres pga. nettets simple geometri, og først i 1982-85 kom, der igen liv i forskningen, da Hopfield, Rummelhard og McClelland og andre fandt på nye netstrukturer og indlæringsalgoritmer.
Simplifikationen fra biologisk neuron til en binærneuron er enorm, idet at neuron input til output funtionen er nonlinear, og langt fra en stepfunktion. En virkelig neuron summerer ikke inputtet, men kan udføre logiske operationer i dendrittræet, en neuron outputter ikke en konstant værdi, men et signal gennem tiden, ligeledes bliver neuroner ikke opdateret synkront men asynkront.
Derfor generaliseres neuronernes output til at antage en værdi i
[-1,1], og neuronresponset til 
,
hvor f er en nonlinear funktion, fx 
, hvor
justerer hældningen af funktionen, der har betydning
for hvor stærkt tvivlende neuroner bliver tvunget til at vælge
side.
Jeg vil i det følgende beskrive et feedforward net med input-lag, output-lag, samt et skjult lag mellem input og output, indeksnotationen er som følger, indeks forneden er et indeks, der tager en heltalig værdi, samtidigt med at det er en label for de 3 lag, et indeks foroven er kun en label.
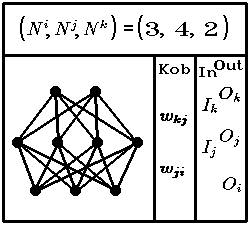
i er et indeks på en neuron i input-laget, analogt er j,k er
et indeks i hhv. det skjulte lag og output-laget, de tre indekser
løber fra 0 til hhv. 
, der er antallet af neuronerne i
de tre lag, I er et input og O er et output, dvs. 
ikke er
defineret mens 
er inputtet til den anden neuron i det
skjulte lag, og 
er inputtet til den anden neuron i
output-laget, og 
er outputtet af den tredie neuron i
input-laget. Alle neuroner i inputlaget er forbundne til alle neuroner i det
skjulte lag. Forbindelsernes styrke er givet ved matricen 
, og
analogt er 
en anden matrix, der giver koblingerne fra der
skjulte lag til output-laget.
For at undgå den asymmetri som neuronernes grænseværdi
giver i neuronrespons ligningen, defineres
, dvs. at 
er
grænseværdien for den anden neuron i det skjulte lag.
er udefineret, 
er givet af brugeren
(inputtet til nettet), og 
er nettets svar, det
er givet ved:
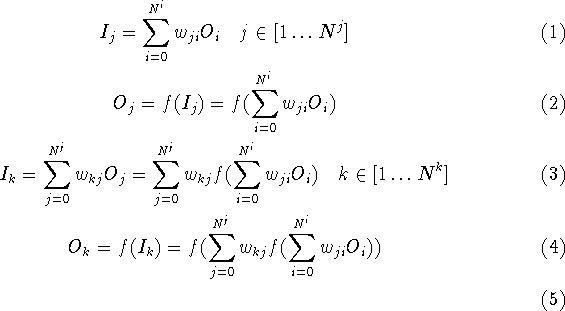
Det vil sige, at nettet er givet entydigt ved koblingsmatricerne
og , og er fjendens spørgsmål 
er nettets
svar givet ved 
, problemet er nu, hvis man kender 
testeksempler, dvs. input 
og deres tilhørende
korrekte output 
, hvordan finder man da koblingsstyrkerne i
nettet så det giver det rigtige svar?
Man begynder med et net hvor alle koblinger er tilfældige, man kan så finde fejlen for indlæringseksemplerne, og indlære nettet ved at føre fejlen tilbage fra output til input-laget, og ændre koblingerne så nettets svar bliver mere og mere korrekt.
Dette gøres fx som følger; man kan for eksempel definere
fejlen for et net 
ved:
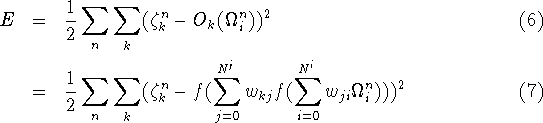
der er en positiv funktional, der antager sit globale minimum for de korrekte koblings matricer, hvis man er til (statistisk) fysik, kan man kalde E for energien.
Minimummet kan nu for eksempel findes ved gradient nedstigning, der i
en dimension forgår ved, at man finder hældningen af en
funktion. Er hældningen positiv er minimummet til venstre, og man
tager et skridt til venstre og prøver igen, dvs. 
vil konverger mod et minimum (ikke nødventigvis et
globalt!), populært udtrykt tager man på skitur i
energilandskabet.
I nettet svare hver kobling til en retning så
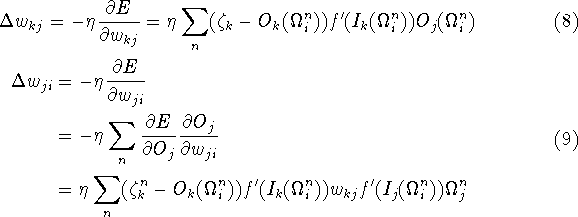
Parameteren 
bestemmer hvor store ændringerne skal
være. Er lille for små ændringer, konvergere koblings
matricerne langsomt, er for stor vil matricerne konvergere
langsomt, fordi de oscillere om minimummet (overskyder), et trick kan
være at bruge et vægtet gennemsnit fx 
, idet oscillationer da dæmpes.
Dette er et eksempel på et neuralt net, som kan generaliseres til flere skjulte lag, eller helt andre strukturer end lagdelte, eller med forbindelser tilbage i nettet, andre fejl funktionaler, bedre konvergerende metoder for at finde minimum (fx Newton's metode eller conjugate gradient descent), indlæringsparameteren kan varieres, så den er stor i begyndelsen. Samt der er det interesante problem at finde den bedste netstruktur til en bestemt opgave, samt hvordan input skal repræsenteres for at nettet kan indlæres hurtigst.
Hvis en opgave skal løses, vil en algoritme altid være det hurtigste, men hvis en algoritme ikke kan findes, eller det vil tage lang tid at finde den, kan neurale net anvendes, idet de kan indlæres ved eksempler, og generalisere de indlærte eksempler til at svare rigtigt på eksempler, de ikke er blevet indlært med.
Opgaver neurale net kan bruges til er fx deling af ord i stavelser, fonetisk opdeling af ord, kunstig intelligens til spil, aflæsning af adresser på konvolutter, tale og billedgenkendelse, signalfiltrering, billedkomprimering og opgaver, der endnu ikke er formulerede, hvor neurale net også kan bruges.
Ulempen ved neurale net er, at det er fra svært til umuligt, at konvertere koblingerne til en algoritme eller identificerbare tilstande, fx hvis man laver et neuralt net der kan addere 2 tobit tal, er det næsten umuligt at lære det en algoritme, der kan addere binære tal.