
Carsten Svaneborg E-post: zqex@@fys.ku.dk
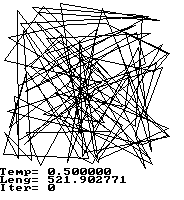
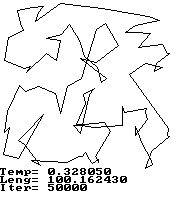
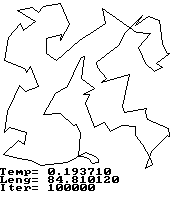
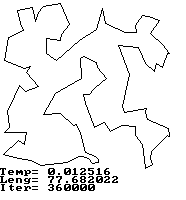
Et typisk ``besværligt'' problem er travelling salesman problemet (TSP), hvor en handelsrejsende skal besøge N byer, på en sådan måde at den handelsrejsende rejser den korteste/hurtigste rute, og starter fra og slutter i sin hjemby, i realistiske problemer vil der envidre være ekstra betingelser, fx at kun visse byer er forbundne, eller der er fartbegrænsninger på vejen mellem byerne, eventuelt skal lasten omlastes for at kunne transporteres ad visse veje, eller der er køretids bestemmelser, eller der er morgen/aften trafik der skal inkluderes. Der er en simplifikation af problemet, som folk der indsamler mælk, planlægger bus/fly/færge ruter, shipping agenter, programmer der laver printplader eller chips, eller bil fabrikanter, og mange andre skal løse.





TSP er et af mange, hvor man ønsker at finde det globale minimum for
en eller anden ikke linær funktion, der afhænger af mange
(evt. diskrete) variable, og som regel vil der være få eller kun ét
globalt minimum, og mange lokale minimaer, så de kan ikke løses
analytisk, og mange er så komplekse, at de ikke engang kan løses på en
computer inden for en realistisk tidshorisont. Det gælder problemer,
hvor antallet af udregninger ![]()
![]() eller N!, hvor N er
``størrelsen'' af problemet. Da det umuligt at finde den bedste
løsning, søger man istedet efter én god løsning inden for en rimelig
tid. Jeg vil her præsentere to algoritmer af typen ``guided random
search'' til at finde globale minimummer; simuleret udglødning, og
genetiske algoritmer, der af naturen er opfundet hhv. i fysik og
biologi
eller N!, hvor N er
``størrelsen'' af problemet. Da det umuligt at finde den bedste
løsning, søger man istedet efter én god løsning inden for en rimelig
tid. Jeg vil her præsentere to algoritmer af typen ``guided random
search'' til at finde globale minimummer; simuleret udglødning, og
genetiske algoritmer, der af naturen er opfundet hhv. i fysik og
biologi![]() .
.

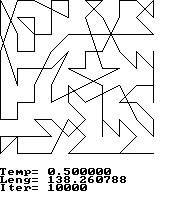
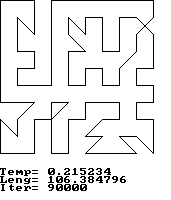
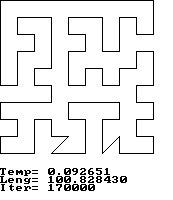
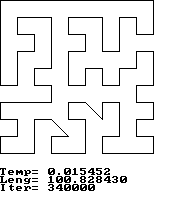
Lad ![]() være en tilstand af systemet, og
være en tilstand af systemet, og ![]() mængden af et
systems tilstande. For en given tilstand
mængden af et
systems tilstande. For en given tilstand ![]() definer
definer ![]() naboklassen til
naboklassen til![]()
![]() . For TSP med N byer er
antallet af tilstande
. For TSP med N byer er
antallet af tilstande ![]() , og en tilstand er af formen
, og en tilstand er af formen
![]() , der fortæller i hvilken rækkefølge
byerne skal besøges, og
, der fortæller i hvilken rækkefølge
byerne skal besøges, og ![]() .
.
Naboklassen kan fx defineres som en ombytning mellem det i'te og j'te element i tilstandsvektoren, hvor i og j er tilfældigt valgte, men intuitionen er, at der skal mange heldige ombytninger til, at løse en rute, der fx krydser sig selv, en bedre defination er blokinversion, hvor en del af ruten besøges i bagvendt rækkefølge, og blokflytning hvor en del af ruten, bliver flyttet til et tidligere/senere sted i rejseplanen.
Det er vigtigt at bruge intuitionen når naboklassen defineres, så den er skræddersyet til problemet, der skal løses, intuitionen for TSP er, at der er praktisk at den næste by altid er i nærheden, så man ikke skal over åen for at hente vand, blokflytning er designet til at løse det problem, og et andet problem er krydsende ruter, idet en ikke krydsende rute altid vil være kortere, og det er klart at to vilkårlige tilstande kan forbindes ved succesive blokinversioner og blokflytninger, så hele tilstandsrummet kan nås fra en vilkårlig starttilstand.
Lad ![]() være positionen på den n'te by, vi kan så definere en
fejl eller energi funktional ved
være positionen på den n'te by, vi kan så definere en
fejl eller energi funktional ved
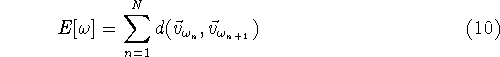
Hvor d er et passende mål for afstanden, fx euklidsk afstand, tiden
det tager - eller energien det kræver, at komme fra by i til
j. Eventuelle ekstra betingelser af formen ![]() , kan klares
ved at addere et straffeled af formen
, kan klares
ved at addere et straffeled af formen ![]() , som hæver
energien af tilstande, der ikke opfylder betingelserne,
, som hæver
energien af tilstande, der ikke opfylder betingelserne, ![]() er en
(Lagrange Multiplier) parameter, der bestemmer hvor streng betingelsen
skal opfyldes.
er en
(Lagrange Multiplier) parameter, der bestemmer hvor streng betingelsen
skal opfyldes.
Algoritmen (forslået af Metropolis et al. i 1953) er som følger:
| 1 | n=0; Start med et tilfældigt valgt tilstand |
| 2 | :loop |
| 3 | Vælg en tilfældig nabo |
| 4 | Sæt |
| | |
| ellers | |
| 5 | n=n+1; if not færdig then goto loop. |
I algoritmen er ![]() den sandsynlighedsfordeling, som man
ønsker at sample tilstandsrummet med, og T en kontrolparameter, der
bruges til at drive algoritmen mod den ønskede sluttilstand, i en
fysisk simulation, hvor man ønsker at finde grundtilstanden, er T
temperaturen
den sandsynlighedsfordeling, som man
ønsker at sample tilstandsrummet med, og T en kontrolparameter, der
bruges til at drive algoritmen mod den ønskede sluttilstand, i en
fysisk simulation, hvor man ønsker at finde grundtilstanden, er T
temperaturen![]() , og
, og
![]() , fordi tilstandene da vil være
Boltzmann fordelt, og når man sænker temperaturen vil sandsyneligheden
for at finde systemet i minimums energitilstande vokse, da alle andre
tilstande vil være eksponentielt undertrykte, man vil da vælge
tilstanden med
, fordi tilstandene da vil være
Boltzmann fordelt, og når man sænker temperaturen vil sandsyneligheden
for at finde systemet i minimums energitilstande vokse, da alle andre
tilstande vil være eksponentielt undertrykte, man vil da vælge
tilstanden med ![]() , hvor
, hvor ![]() , og oftest kan
, og oftest kan ![]() findes uden at
beregne den totale energi, og derved bliver algoritmen meget mere
effektiv.
findes uden at
beregne den totale energi, og derved bliver algoritmen meget mere
effektiv.
Mens algoritmen kører sænkes temperaturen gradvist, ![]() er
temperaturen ved n'te iteration, skal algoritmen køre N
iterationer kan
er
temperaturen ved n'te iteration, skal algoritmen køre N
iterationer kan ![]() fx vælges som
fx vælges som ![]() eller
eller
![]() , parametrene estimeres fra at
, parametrene estimeres fra at ![]() start
temperaturen skal være sammenlignelig med den største energibarriere,
og
start
temperaturen skal være sammenlignelig med den største energibarriere,
og ![]() skal være af samme størrelsesorden, som den mindst mulige
energi. Men en effektiv adaptiv annealing schedule kan findes, givet
ved termodynamiske størrelser, der kan udregnes samtidigt med at
algoritmen kører (konstant termodynamisk hastighed)
skal være af samme størrelsesorden, som den mindst mulige
energi. Men en effektiv adaptiv annealing schedule kan findes, givet
ved termodynamiske størrelser, der kan udregnes samtidigt med at
algoritmen kører (konstant termodynamisk hastighed)![]() .
.
Algoritmen vil, hvis den finder et lokalt minimum, have en vis sandsynelighed for at krydse energibarrieren til et bedre (måske globalt) minimum, hvis man ikke køler for hurtigt, dvs. hvis algoritmen er i et lokalt minimum skal temperaturen holdes over den energibarriere, der er omkring minimummet.
Simuleret udglødning er inspireret af statistisk fysik, der er i
sving bl.a når fysiske systemer afkøles, hvis ![]() vil det være en tilfældig søgning og sandsynligheden for at
finde et globalt minimum er minimal, men ved høj temperatur kan
alle energibarriere krydses, hvis
vil det være en tilfældig søgning og sandsynligheden for at
finde et globalt minimum er minimal, men ved høj temperatur kan
alle energibarriere krydses, hvis ![]() (Quenching)
vil algoritmen blive fanget i det første minimum den finder
(sandsyneligt et lokalt energiminimum), det svarer til en
hærdningsprocess, fysisk svare det til en pludselig afkøling
af smeltet metal, hvorved det bliver meget stift men sprødt,
pga. den polykrystalinske struktur det får, en langsom afkøling
vil give systemet tid til at finde et globalt minimum, det svare
til metallet er et perfekt krystal, hvor metallet vil
være elastisk og deformerbart.
(Quenching)
vil algoritmen blive fanget i det første minimum den finder
(sandsyneligt et lokalt energiminimum), det svarer til en
hærdningsprocess, fysisk svare det til en pludselig afkøling
af smeltet metal, hvorved det bliver meget stift men sprødt,
pga. den polykrystalinske struktur det får, en langsom afkøling
vil give systemet tid til at finde et globalt minimum, det svare
til metallet er et perfekt krystal, hvor metallet vil
være elastisk og deformerbart.