Jørn B. Olsson
Sidste år viste George Andrews (Penn State University) mig tre
identiteter, som jeg gerne vil præsentere her. De kan forstås som
identiteter i ringen 
af formelle potensrækker med
heltallige koefficienter. Her er identiteterne:
Identiteten (A1) stammer fra Euler, (A3) forekommer i et arbejde af Andrews (Proc. Glasgow Math. Soc. 8 (1967), 33-40), hvorimod (A2) vist har premiere her i Famøs.
Vi vil starte med at forklare, hvordan de uendelige summer kan
opfattes som elementer i . Derefter vil det blive
forklaret, hvordan de kan bevises kombinatorisk med nogle simple
optællingsargumenter for partitioner. Det er forbavsende let.
Identiteter som (A1)-(A3) kan ofte også bevises ``analytisk''. Det
vil vi sige lidt om til slut.
Ringen 's elementer er formelle potensrækker, dvsformelle summe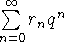r 
,
hvor 
, 
. Man kan addere og
multiplicere sådanne formelle potensrækker på samme måde som man
gør ved polynomier. Således er for eksempel
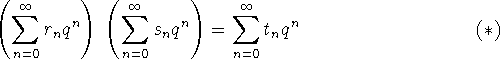
hvor 
.
Hermed fastlægges så en kommutativ ringstruktur på .
Et
element x i en ring kaldes som bekendt invertibelt, hvis der findes
et element 
i ringen som opfylder xy=yx=1. På grund
af
gradformlen for polynomier har den sædvanlige polynomring 
kun 2 invertible elementer, nemlig de konstante polynomier 1 og
-1. Men i potensrækkeringen ser det helt anderles ud.
Der gælder
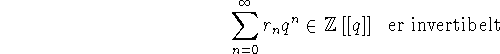
hvis og kun hvis 
. Dette er ikke svært at bevise. Vi har
for eksempel, at 1-q er invertibelt i og
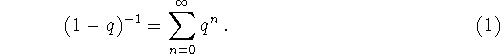
fordi hvis man multiplicerer (1-q) og 
ved
hjælp af (*), fås potensrækken 
. Nu kan vi også forklare, hvorfor de enkelte summander
på venstresiderne af (A1)-(A3) er elementer i . For
eksempel er summanden for k=4 i (A1) (under anvendelse af (1))
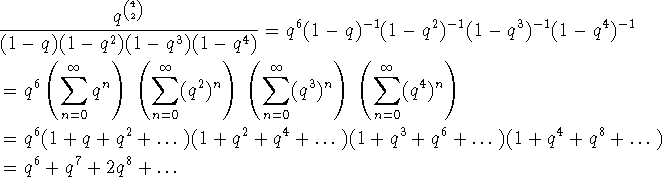
Vi mangler stadig at forklare, hvordan de uendelige summer i
(A1)-(A3) kan opfattes som elementer i . Pointen er, at
der for et givet 
kun er endelig mange summander i den
uendelige sum, hvor koefficienten til 
er forskellig fra 0!
Den k'te summand i (A1) starter for eksempel med 
og giver derfor højst bidrag til når 
. Der er altså for givet n højst endelig mange sådann
e
k, så koefficienten til i den uendelige sum er den samme som
i den endelige sum
Som et konkret eksempel er koefficienten til 
på venstre side
af (A1) lig koefficienten til i potensrækken
som ses at være
Vi vil nu forklare, at summanderne i (A1) (bortset fra
fortegnene 
er ``frembringende funktioner'' for antallet af
partitioner med visse egenskaber. Hvis 
er følge af hele tal
kaldes elementet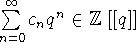 
for
den frembringende funktion for følgen.
En endelig sekvens 
af
naturlige tal som opfylder 
og
kaldes en partition af n. Tallene
kaldes partitionen 
's dele. Vi lader
p(n) være antallet af partitioner af n og p(n,r) antallet af
partitioner af n, hvis dele alle er 
. Vi kan angive en
frembringende funktion for følgen 
:
Bevis. Det er ofte en fordel at benytte en ``eksponentiel''
skrivemåde for partitioner. Hvis 
er ikke-negative
hele tal betegner 
den partition af
som starter med 
dele, der alle er
lig k, efterfulgt af 
dele (k-1) osv, sluttende med
dele 1. Tallene kan altså ses som
multipliciteterne af de enkelte dele. Betragt
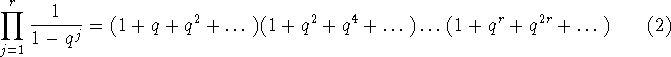
Hvis vi beregner koefficienten til ved at multiplicere
paranteserne ud, ser vi, at denne koefficient er lig antallet af
måder, man kan fremstille n som
hvor 
. En sådan fremstilling svarer til at vi
har multipliceret summanderne 
,
hvor 
kommer fra den i'te sum i (2). Fra
fremstillingen (3) får vi også partitionen 
som har alle dele . Hermed er lemmaet bevist.
Ved et lignende argument kan man overbevise sig om at
,
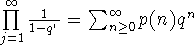som er en velkendt identitet.
Vi lader nu d(n,k) være antallet af partitioner
af n, hvor
(altså partitioner af n i præcis
k forskellige dele). Bemærk at i en sådan partition er 
, 
, så d(n,k)=0 når 
. Hvis k' er det største naturlige tal med
, er altså d(n,k')=0!
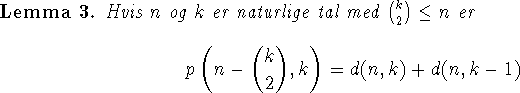
Bevis. Vi angiver et bijektivt bevis ved hjælp af partitionerne. Lad
være en partition af 
skrevet eksponentielt. For
sættes
Så er 
. Vi sætter så
og
( 
er her skrevet i normal skrivemåde!) Det er klart, at
er en partition af n i forskellige dele. På den anden side
kan vi, hvis er en vilkårlig partition af n i k eller
k-1 forskellige dele 
, bruge formlerne (4) som et
triangulært ligningssystem med som ubekendte.
Løsningen 
giver så multipliceterne for en
partition af med dele 
. Hermed er vist, at
afbildningen 
er en bijektion.
Bemærkning Det er af praktiske grunde almindeligt at tælle den ``tomme'' partition (0) som en partition af n=0. Det betyder, at p(0,0)=d(0,0)=1, således at Lemma 3 også har mening og er korrekt, når n=0 eller k=0, idet selvfølgelig d(n,a)=0 fo r n>0 og per definition d(n,-1)=0 for alle n.
Bevis for (A1). Vi viser, at
Ifølge Korollar 2 og Lemma 3 er
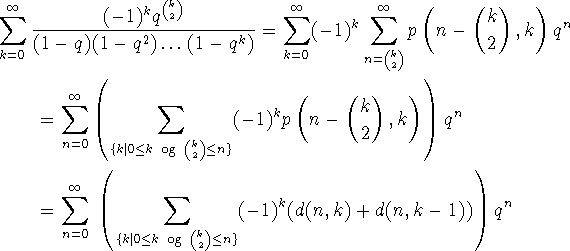
Hvis vi for et givet n lader k' være det største hele tal med
, så er
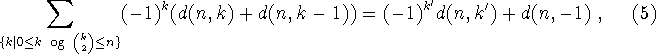
idet de andre led forkortes parvis. Men ifølge tidligere bemærkninger er d(n,k')=0 og d(n,-1)=0, så den alternerende s um (5) er 0. Heraf følger resultatet.
Beviserne for (A2) og (A3) benytter samme princip.
Skitse af bevis for (A2) Lad u(n,2k+1)
være antallet af partitioner af n i ulige dele 
, og
e(n,2k+1) antallet af partitioner af n i ulige dele ,
hvor 
alle har positiv multiplicitet. Vi har så at
koefficienten til i 
er
. Man beviser bijektivt at
ved at afbilde partitionen
i
(Bemærk, at 
).
Skitse af bevis for (A3) Da 
ser vi, at koefficienten til i 
er
, hvor 
( 
) er antallet af
partitioner af n i et lige (ulige) antal dele . Idet vi
lader 
( 
) være antallet af partitioner
af n i k forskellige dele, hvor
er lige (ulige) kan vi bruge bijektionen fra Lemma 3's
bevis til at opnå relationerne:
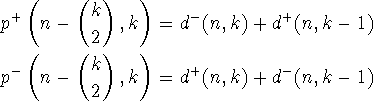
Så vil igen leddene i koefficienten til på venstre side af
(A3)
forkortes parvis.
Man kan måske få den idé, at (A1)-(A3) er specielle tilfælde af
en
mere generel identitet, og det er rigtigt. Ud over q er man nødt
til at tilføje en ny variabel t og arbejde i 
. Der
gælder
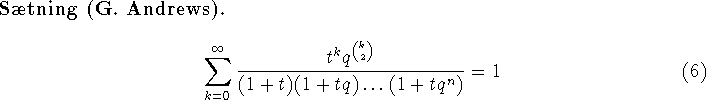
Andrews har givet et ``analytisk'' bevis for dette. Den ovenstående sum betragtes som en funktion f(t) af t og er som sådan analytisk i t omkring t=0. Endvidere kan man let beregne, at f(t) opfylder relationen
Da den konstante funktion 1 også er analytisk og opfylder (7), kan man slutte, at f(t)=1.
Identiteten (A1) opnås ved at gange identiteten (6) med (1+t) og så
sætte t=-1. (A2) opnås ved at erstatte q med 
i (6), og så
sætte t=-q. (A3) opnås ved at sætte t=1, og så gange med
2.
Om man vil anvende en kombinatorisk eller analytisk metode til at forklare en given identitet afhænger af omstændighederne. Begge metoder har deres fordele og ulemper.