Rasmus Borup Hansen
I de fleste former for naturvidenskab optræder der ofte lineære
sammenhænge, dvs. sammenhænge mellem x og y på formen y=ax+b.
En gymnasieformelsamling for fysik byder på adskillige af slagsen
(hvor endda flere af dem er endnu simplere, idet b=0), og de dukker
også op i fag som økonomi, datalogi, biologi, kemi og psykologi --
alle steder hvor der er noget, der kan måles. Man er tit interesseret
i at undersøge sådan et lineært fænomen (eller undersøge, om det
overhovedet er lineært), og man laver derfor en række målinger
![]() . Udfra disse k talpar er
man så interesseret i at finde de ukendte koefficienter a og b. Da
målinger som regel er behæftet med en vis usikkerhed, kan man ikke
gøre sig forhåbninger om at finde en løsning, der passer perfekt --
det eneste man kan gøre, er at forsøge at finde den ``bedst mulige''
løsning. Sagt geometrisk er problemet altså at finde den rette linje,
der i en eller anden forstand kommer tættest på de k observerede
punkter.
. Udfra disse k talpar er
man så interesseret i at finde de ukendte koefficienter a og b. Da
målinger som regel er behæftet med en vis usikkerhed, kan man ikke
gøre sig forhåbninger om at finde en løsning, der passer perfekt --
det eneste man kan gøre, er at forsøge at finde den ``bedst mulige''
løsning. Sagt geometrisk er problemet altså at finde den rette linje,
der i en eller anden forstand kommer tættest på de k observerede
punkter.
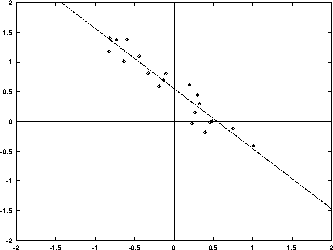
Figur 1: Linje fundet ved de mindste kvadraters metode
Problemet blev diskuteret af flere matematikere i det 18. århundrede,
primært i forbindelse med astronomiske observationer. Den metode, som
vi i dag anser for at være den bedste, er de mindste kvadraters
metode, som blev udviklet af Legendre (1752-1833) i 1805. Metoden
går ud på at finde den linje, hvor kvadratet på den lodrette afstand
mellem punkterne og linjen er mindst mulig. Der er to ting, der kan
forekomme en smule mærkværdigt ved denne metode. Hvorfor betragter man
den lodrette afstand i stedet for blot afstanden, og hvorfor tager man
kvadratet på den lodrette afstand i stedet for blot den lodrette
afstand? Svaret er simpelt: Udregningerne bliver simplest, og man når
frem til den pæneste formel ved at gøre netop sådan. Hvis man vælger
at arbejde med afstanden frem for den lodrette afstand, bliver de
ligninger, man skal løse, ganske uoverskuelige, og hvis man ikke tager
kvadratet, løber man ind i problemer, fordi ![]() er
differentiabel mht. x, mens
er
differentiabel mht. x, mens ![]() ikke er differentiabel i
ikke er differentiabel i
![]() . Endelig får løsningen nogle pæne statistiske egenskaber, hvis
man betragter summen af kvadraterne på de lodrette afstande. Figur
2 viser et eksempel på en linje fundet vha. de mindste
kvadraters metode.
. Endelig får løsningen nogle pæne statistiske egenskaber, hvis
man betragter summen af kvadraterne på de lodrette afstande. Figur
2 viser et eksempel på en linje fundet vha. de mindste
kvadraters metode.
Kort tid efter at Legendres opdagelse i 1805 blev metoden brugt i stort omfang til at løse astronomiske og geodætiske problemer. Specielt blev den brugt af Gauss (1777-1855) i 1809, der ikke citerede Legendre for opdagelsen men i stedet hævdede, at han selv havde brugt metoden lige siden 1795. Legendre følte sig krænket og holdt fast ved, at det må være den person, der først publicerer et videnskabeligt resultat, der må krediteres for dets opdagelse. Skænderiet varede ved i nogle år, og så sent som i 1827 bebrejdede Legendre stadig Gauss for at tilegne sig hæder for andres opdagelser.
Lad os et øjeblik kaste os over matematikken bag de mindste kvadraters
metode. Hvis vi har en mistanke om, at punkterne ![]() er observationer af det lineære fænomen y=ax+b, kan vi
finde estimater for a og b ved at minimere summen af
afstandskvadraterne (i alle summer løber i fra 1 til k)
er observationer af det lineære fænomen y=ax+b, kan vi
finde estimater for a og b ved at minimere summen af
afstandskvadraterne (i alle summer løber i fra 1 til k)

der differentieret mht. til a hhv. b giver

Idet de to sidste størrelser er minimal, når summen af afstandskvadraterne er nul, kan vi finde a og b ved at løse to ligninger med to ubekendte. Af den sidste fås let, at
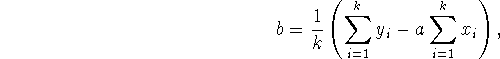
og af den første fås, at

der ved indsættelse af udtrykket for b og lidt omrokkering giver, at
Hvis man har haft (eller har) Statistik 0, vil man muligvis kunne genkende disse udtryk; det er nemlig også dem, man når frem til ved at anvende maksimaliseringsestimatorteori.
De mindste kvadraters metode virker fortrinligt, når der rent faktisk
er tale om en lineær sammenhæng, hvilket figur 2 og
2 illustrerer, og hvis man skal undersøge sammenhænge på
formen ![]() eller
eller ![]() , kan man udnytte, at der gælder
, kan man udnytte, at der gælder ![]() og henholdsvis
og henholdsvis ![]() , ligesom når
man anvender logaritmisk eller dobbelt-logaritmisk papir.
, ligesom når
man anvender logaritmisk eller dobbelt-logaritmisk papir.

(a) y afhænger ikke af x.
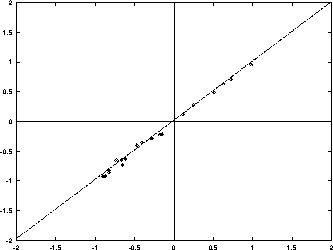
(b) y=x.
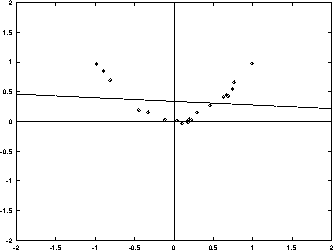
(c) Metoden virker ikke for ![]() .
.
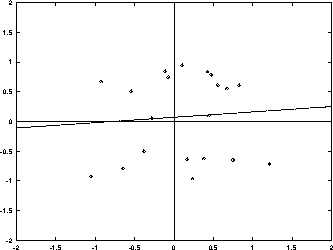
(d) Der er ingen lineær sammenhæng.
Figur 2:Eksempler på anvendelser af mindste kvadraters metode til empirisk undersøgelse af lineære sammenhænge.
Der er intet i vejen for at anvende samme metode på andre sammenhænge
end netop de lineære. En umiddelbar generalisering er til polynomier
af grad n, ![]() , og her bliver man nødt til at
løse n ligninger med n ubekendte:
, og her bliver man nødt til at
løse n ligninger med n ubekendte:
Det var sådan nogle problemer, der fik Gauss til at udvikle metoden ``Gauss-elimination'', som man lærer om på Matematik 1.
Man kan nemt komme ud for, at man ikke kan lave udregningerne i de
mindste kvadraters metode eksakt. Man kan f.eks. betragte den
harmoniske svingning ![]() . Den giver anledning
til tre ikke-lineære ligninger med tre ubekendte, der bestemt ikke
lader sig finde nemt. Men når vi nu alligevel arbejder med data, der
er behæftet med måleusikkerhed, er der intet i vejen for at anvende
numeriske metoder til at løse ligningerne. F.eks. kan man anvende
Newton-Raphsons iterationsformel
. Den giver anledning
til tre ikke-lineære ligninger med tre ubekendte, der bestemt ikke
lader sig finde nemt. Men når vi nu alligevel arbejder med data, der
er behæftet med måleusikkerhed, er der intet i vejen for at anvende
numeriske metoder til at løse ligningerne. F.eks. kan man anvende
Newton-Raphsons iterationsformel ![]() ,
der er kendt fra Gymnasiet. Men når vi arbejder i flere dimensioner,
er vi imidlertid nødt til at skrive den på formen
,
der er kendt fra Gymnasiet. Men når vi arbejder i flere dimensioner,
er vi imidlertid nødt til at skrive den på formen
![]()
Hvis ![]() er
afstandskvadratsummen, er
er
afstandskvadratsummen, er
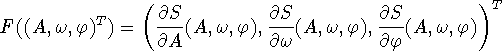
og F' er jacobianden (differentialkvotienten) for F. Da allerde F er temmelig omstændig at skrive ned, når man udregner de tre differentialkvotienter, bliver jacobianden endnu værre. Med lidt hjælp fra f.eks. computerprogrammet Maple kan den imidlertid udregnes til

hvor ![]() ,
, ![]() og
og
![]() (af pladshensyn er argumenterne A,
(af pladshensyn er argumenterne A,
![]() og
og ![]() udeladt).
udeladt).
Hvis ![]() ,
, ![]() og
og ![]() er det første gæt på
en løsning, kan man udregne korrektionsvektoren
er det første gæt på
en løsning, kan man udregne korrektionsvektoren ![]() udfra
ligningen
udfra
ligningen
![]()
Da ![]() er en
er en
![]() -matrix, og
-matrix, og
![]() er en
er en
![]() -matrix, er der her tale om tre lineære ligninger
med tre ubekendte, der kan løses vha. Gauss-elimination. Når man har
fundet
-matrix, er der her tale om tre lineære ligninger
med tre ubekendte, der kan løses vha. Gauss-elimination. Når man har
fundet ![]() kan man udregne det næste løsningsgæt
kan man udregne det næste løsningsgæt ![]() og gentage hele proceduren indtil
f.eks. længden af korrektionsvektoren bliver tilstrækkelig lille. I
modsætning til tilfældet med polynomier skal man være opmærksom på, at
der ikke er nogen entydig løsning, da f.eks.
og gentage hele proceduren indtil
f.eks. længden af korrektionsvektoren bliver tilstrækkelig lille. I
modsætning til tilfældet med polynomier skal man være opmærksom på, at
der ikke er nogen entydig løsning, da f.eks.
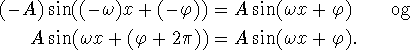
Desuden kan man -- pga. sinus's periodiske natur -- komme
ud for, at man kun finder et lokalt minimum (eller, hvis man er
uheldig, et maksimum) vha. den ovenfor skitserede metode. Det er
derfor en god idé at tegne grafen for den fundne funktion sammen med
måledata, så man kan finde et godt start-gæt og vurdere, om løsningen
er fornuftig. Figur 2 viser nogle målinger (med
usikkerhed) fra en harmonisk svingning med parametre A=1,5,
![]() og
og ![]() . Ud fra start-gættet A=1,
. Ud fra start-gættet A=1, ![]() og
og
![]() fandt et computer-program, der anvendte de mindste kvadraters
metode og Newton-Raphson-metoden, frem til parametrene A=1,496,
fandt et computer-program, der anvendte de mindste kvadraters
metode og Newton-Raphson-metoden, frem til parametrene A=1,496,
![]() og
og ![]() . Kurven på figur 2 er
grafen for en harmonisk svingning med disse parametre.
. Kurven på figur 2 er
grafen for en harmonisk svingning med disse parametre.
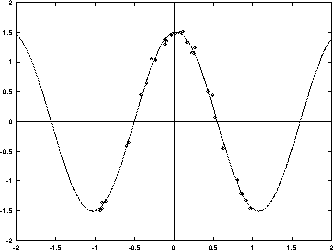
Figur 3: Målinger fra harmonisk svingning samt grafen for en
harmonisk svingning fundet vha. de mindste kvadraters metode.