Foregående: Matematik på Internet Op: FAMØS december 1996 Næste: Litteratur

Legitimering af infinitessimalerne på den reelle linie

Mai Gehrke

Problemet med at analysere kontinuerte processer har en lang historie, som går tilbage i hvert fald til det klassiske Grækenland, som set for eksempel i Zenons paradokser. På trods af denne lange historie, skete der forholdsvis få fremskridt af generel natur før den anden halvdel af det 17. århundrede. Gennem århundrederne var en lang række specifikke arealer, volumener, tangenter, og lignende størrelser blevet udregnet med ad hoc metoder. Meget få generelle redskaber blev udarbejdet i perioden, der varede helt op igennem middelalderen. Nogle generelle ideer var der dog, såsom Archimedes Egenskab:

Denne egenskab er vigtig, for eksempel når vi integrerer, da den sikrer os at, for vilkårligt større end nul, kan vi dække ethvert endeligt interval med endeligt mange delintervaller af længde .

I det 17. århundrede blev der udarbejdet en generel integral- og differentialteori af Newton og, lidt senere men uafhængigt, af Leibniz. Nogle af Newton's beviser var for det meste baserede på brugen af et slags vagt grænsebegreb eller på fysisk intuition. Leibniz' teori var baseret på brugen af infinitessimaler. En infinitessimal er et tal, der er tættere på 0 end for , og betyder, at forskellen mellem x og y er infinitessimal. Ved at antage at sådanne infinitessimaler eksisterede, kunne han definere differentialkvotienten som en rigtig kvotient:

Hans generelle teori reducerede analyse til en infinitessimalkalkyle, som gjorde løsningen af problemer mere algoritmisk. Dette medførte meget store fremskridt inden for en meget kort tidsperiode blandt Leibniz' efterfølgere.

Det gode ved disse metoder, bortset fra at gøre løsningsprocesserne mere algoritmiske, var også, at intuitionen, der hører med til denne abstraktion, passer godt til den måde, vi tænker på kontinuerte processer på. For eksempel bliver kontinuitet af f i x til:

hvilket må siges at være en hel del tættere på vores intuitive ide om kontinuitet end den definition, vi nu er vant til: For hvert epsilon større end nul eksisterer der delta større end nul...

Men desværre var der fundamentale problemer med disse idéer. Her illustrerer vi nogle af de typiske problemer, som opstod ved brugen af infinitessimaler:

1. Tag funktionen . Efter Leibniz' definition har vi, at . Af dette skal vi selvfølgelig slutte at f'(0)=0. Det vil sige at vi først ser på infinitessimalerne som forskellige fra 0 og derefter, når det passer os, som lig med nul. Det må jo siges at være dårlig matematisk praksis. Til gengæld kan vi nok godt forestille os fra vores moderne synspunkt, at dette ikke er så svært at råde bod på med en ækvivalensrelation.
2. Men der er nu meget værre problemer. For at kunne nå de rette slutninger, og også fra et rent intuitivt synspunkt, er det nødvendigt at have følgende egenskab for infinitessimaler:

   

   Men det vil jo sige at de reelle tal, som inkluderer infinitessimalerne, ikke længere har den Archimediske egenskab. Selvfølgelig har man stadigvæk brug for Archimedes' egenskab, når man bruger disse metoder, og den gjorde Leibniz og hans efterfølgere da også frit brug af når de ville, selvom det var helt klart, at der var andre situationer, hvor det ikke duer at bruge den...

3. Der er andre problemer af denne art. Eksistensen af infinitessimaler strider også mod fuldstændighedsegenskaben af de reelle tal: Mængden bestående af alle infinitessimalerne, , som Leibniz kaldte monaden omkring 0, er helt klart en opadtil begrænset mængde! Derfor, hvis mængden af de reelle tal har fuldstændighedsegenskaben, da må have et supremum. Men hvis , så må der findes så , hvilket medfører at . Dette modsiger at er supremum af mængden af alle infinitessimaler. Så nu er mængden af reelle tal heller ikke fuldstændig længere.

Leibniz efterspurgte et solidt grundlag for sine metoder: En udvidelse af de reelle tal, der inkluderer infinitessimalerne, men som stadig har de egenskaber vi har brug for, når vi laver analyse. Det viste sig, at det skulle vare mange år, før han fik sit ønske opfyldt. Og i mellemtiden var infinitessimalerne for længst blevet smidt ud til fordel for grænsebegreber, som er lidt mere besværlige at have med at gøre, og som ikke svarer helt så godt til vores intuition om kontinuerte processer, men som i det mindste fik grundlaget i orden.

Skeptikeren, eller ikke-matematikeren, kunne jo nu spørge, hvorfor det er så vigtigt at have grundlaget i orden. Det er det ikke altid, men når man er nået et vist stykke ind i teorien, er fordelen ved et sundt grundlag, at man kan lade det matematiske system tage én videre end dér, hvor intuitionen om den praktiske anvendelse af teorien kan lede. Så indtil videre var infinitessimalerne formelt ude af matematikken, selvom de jo nok stadig færdedes i matematikeres hoveder. Det var bare ikke noget man talte højt om - og til en vis grad er det stadig sandt i dag. Men infinitessimalerne har nu fået grundlag for at kunne komme tilbage i folden, og for at kunne forklare dét, må vi først se på en helt anden udvikling inden for matematikken: matematisk logik.

Matematisk logik

Formålet med matematisk logik er at forstå, hvad det er vi laver som matematikere, om det virkelig altsammen hænger ordentligt sammen, og derefter også, hvad mulighederne og begrænsningerne for vore metoder er. Hvad er det så egentlig vi går og laver? Vi studerer matematiske strukturer. Selvom de fleste af os mener, at disse eksisterer på et eller andet plan, er det jo ikke som for fysikere eller kemikere, som kan gå i laboratoriet og begynde at måle og lave forsøg for at forstå deres emne. Vores redskab er deduktiv tankegang - eller logik.

Hvad betyder

Det er der to svar på; ét der svarer til det vi mener vi foretager os. Her ligner vi naturvidenskabmænd - og kvinder:

Semantik: Hver gang er sand i en matematisk struktur, så er det også. Dette noteres .

Det andet svar er nærmere på det, vi rent faktisk foretager os.

Syntaks: kan bevises fra . Her er et bevis en symbolsk algoritme, der bruges til at producere nye sætninger fra gamle. Dette noteres .

For at bevismetoden overhovedet skal være brugbar, er det nødvendigt at

På den anden side, hvis vi som matematikere skal have mulighed for at udvinde alle sande sætninger, så må vi også have

En logik, der har begge egenskaberne, siges at være fuldstændig. Gödel's Fuldstændighedssætning siger, at første-ordens logikken er fuldstændig. Første-ordens logikken er den logik, hvor kvantorer kun løber over grundelementer i de matematiske strukturer og ikke over delmængder eller andre objekter konstrueret over grundelementerne. Det kan også vises, at man essentielt ikke kan gå uden for denne logik og bevare fuldstændighedsegenskaben. Så vi må altså håbe, at vi kan være glade for at leve inden for første-ordens logikken. De fleste er enige om, at alt matematik befinder sig inden for ZFC (Zermelo-Fräenkel mængdeteori med udvalgsaksiomet), så det ser jo ud til, at første-ordens logikken er et godt hjem til os. På den anden side har vi Löwenheim-Skolem's faretruende sætning: Hvis der er en uendelig model af en teori, så er der mange; faktisk mindst én af hver uendelig størrelsesorden større end størrelsen af det alfabet sætningerne i teorien er skrevet i. Det var ikke så godt. Hvis vi vil prøve på at beskrive , de naturlige tal, eller , de reelle tal, inden for første-ordens logikken, så er de ikke entydige strukturer. På samme måde er der så heller ikke en entydig mængdeteori men masser af dem. Det var dog afskyeligt! Nå, men hvis vi kan lade være med at miste modet helt på dette tidspunkt, og løbe hen og stikke hovedet ned i jorden, så kan vi faktisk udnytte denne mangel på entydighed til stor fordel!

Et Eksperiment: Lad være mængden af de naturlige tal med efterfølger operationen og den naturlige orden, og lad være første-ordens teorien af . Fra Löwenheim-Skolem's sætning følger det, at vi har en matematisk struktur , som er en model af , men . Det vil sige at opfylder akkurat de samme første ordens sætninger som , men er ikke isomorf med . Hvordan ser ud? For det første er en ordning på , som kan defineres ud fra på samme måde som er defineret udfra s. Vi har følgende første-ordens sætning opfyldt i :

Derfor er den samme sætning også sand i . Elementet i , som opfylder er selvfølgelig 1; lad os kalde det tilsvarende element i for . På grundlag af dette definerer vi en s-homomorfi med . Da kan defineres ud fra s på N, og da de to strukturer opfylder alle de samme første-ordens sætninger, følger det at er en indlejring - det vil sige at afbildningen er en s-homomorfi, med hvis og kun hvis . Det vil nu sige, at hvis afbildningen * er surjektiv, så er isomorf med . Men da , følger det, at der er . Og da vi har følgende sætning opfyldt i begge strukturer

da må alle de elementer af , som ikke er i *-billedet, være helt ude til højre for *-billedet. Vi opnår nu følgende billede af :

Ved hjælp af lignende argumenter kan vi vise at er uden for billedet af , at , og ikke er inden for rækkevide af hinanden ved hjælp af anvendelser af , og at der mellem hvert par , af sådanne 'uendeligt store' naturlige tal, som er `uendeligt langt' fra hinanden, er et andet uendeligt stort naturligt tal (nemlig for eksempel ), som er mellem dem men uendeligt langt fra dem begge. Vi har nu følgende billede af vores struktur , som ikke kan skelnes fra inden for første-ordens logikken!:

Ikke-Standard Analyse

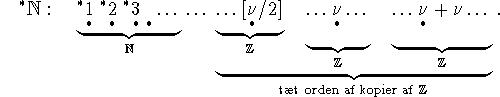
Denne mangel på entydighed inden for første-orden er, hvad man drager fordel af i ikke-standard analyse. Men nu vil vi være lidt mere sofistikerede og også sige noget om højere-ordens strukturen. Til det formål definerer vi højere-ordens strukturen over en mængde R, som værende den disjunkte foreningsmængde:

Nu tager vi til at være teorien af denne struktur i en logik som har konstant-symboler for hvert af 's elementer (dette er ikke præcist, da jeg ikke siger noget om, hvilken slags prædikater eller relationssymboler jeg tager med i min logik. Da det mængdeteoretiske hierarki er `fladet ud' i , er det nødvendigt at have prædikater i sproget, som kan forklare hvordan hierarkiet må rekonstrueres). Som i vores lille eksperiment med tager vi nu til at være en model af . Fordi at alle konstant-symbolerne, som står for elementerne i , er fortolkede i , har vi afbildninger i alle lagene:

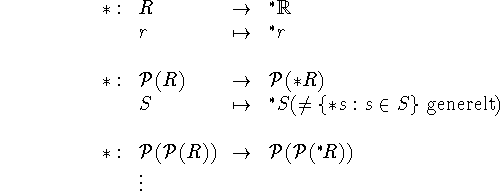
Her skal det forstås sådan at superstrukturen . Det vil sige, at superstrukturen består af foreningsmængden af *-billedet af mængden af alle relationer over R på hvert niveau. Dette er generelt ikke alle relationerne over grundmængden . Vent lidt, og så vil du se i eksemplerne, hvad der menes med dette. Men først kan vi nu definere tre forskellige slags relationer over grundmængden :

Nu kan vi formulere den ovenstående beskrivelse af ved at sige at den består af alle de interne relationer over . Denne situation kan i første omgang synes forfærdelig kompliceret, men det er netop fordi, ikke alle relationer er inde i modellen at det kan lade sig gøre at beholde alle egenskaberne af den originale struktur i den udvidede struktur og så samtidig få ekstra 'ideele elementer' såsom infinitessimalerne. Det, at egenskaberne er bevarede i udvidelsen, svarer til at sige, at er en model af . Dette kan udtrykkes i det følgende princip:

Leibniz's princip:

Lad være en sætning om med hver kvantor begrænset til en vis type relationer i hierarkiet , og den samme sætning om relationerne af samme type i (det vil sige om de interne relationer af pågældende type). Så har vi

Eksempler:

1. Lad og være to relationer i superstrukturen .

   

   Det vil sige, at afbildningen er injektiv på hvert niveau.

2. Lad, for eksempel, . Da kan vi vise at dens *-billede, som er en standard relation over svarende til , er en intern relation af samme type som , og som udvider :

   

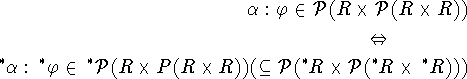
   Så standard relationer er altid interne. At er en udvidelse af , får vi, for hvert , ved hjælp af følgende sætning:

   

3. Lad være en funktion på R. Så er en binær relation på . Men ved brug af Leibniz' Princip kan vi faktisk konkludere, at er en funktion på , som udvider f. Som eksempel på, hvordan dette virker, giver vi:

   

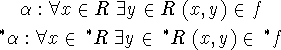
   Vi udelader på elementer, da på grundniveauet er en ægte indlejring. Vi udlader også på funktioner og relationer, da *-billederne er udvidelser af de originale objekter (dette er i overensstemmelse med almindelig matematisk praksis). På mængder derimod beholder vi , da det er tilfældet for enhver uendelig mængde, at *-billedet af mængden er større end mængden, som består af *-billedet af hvert af mængdens elementer.

4. Ved hjælp af argumenter som dem i eksempel (3) kan vi vise, at siden er et ordnet legeme, så er det også.

Disse egenskaber overføres fuldstændigt intakte, fordi de alle er første-ordens egenskaber. På grundniveauet er alle objekterne interne, så vi løber ikke ind i noget usædvanligt. Vi skal snart se, at det går knap så godt (men godt nok - det er pointen) med højere-ordens egenskaber. Men først må vi sørge for, at det ikke er muligt, at de to strukturer simpelthen er identiske. Indtil videre har vi jo ikke sagt noget, som gør at og behøver at være forskellige. Men vi ved fra Löwenheim-Skolem, at der er modeller , som ikke er isomorfe med . Vi kan faktisk bede om lidt mere:

Idealisationsprincip:

Lad være en binær relation et eller andet sted oppe i superstrukturen med domæne A og co-domæne B, som er ``concurrent'' (det vil sige at for hver endelig delmængde , er der et element , så at ). Idealisationsprincippet siger så, at der må være et element med egenskaben at for alle på én gang.

Eksempler:

1. Så snart er en uendelig mængde, så kan vi konkludere, at S indeholder `ideelle' elementer, det vil sige at . Tag relationen på . Den er ``concurrent'', hvis og kun hvis S er uendelig. Da må der, efter idealisationsprincippet, være et element med egenskaben at for alle . Nu skal vi bare være sikre på, at er på , men det følger fra Leibniz' Princip med sætningen

   

   (her er det vigtigt at forstå, at det = tegn, som forekommer her, ikke står for en relation i superstrukturen , men er en del af logikken og derfor er garanteret til at være fortolket som rigtig identitet i alle strukturer)

2. er ``concurrent'' på R, så der er 'uendeligt store' reelle tal i (det vil sige elementer som er større end alle standard elementer af ). Men det burde jo ikke komme som en overraskelse, da jo må indeholde en udvidelse af , som den vi så på i vores lille `eksperiment'.
3. er ``concurrent'' på , så der er infinitessimaler i .
4. Hvert reelt tal har en monade . Dette kan man enten slutte ved at bruge idealisationsprincipet igen med på mængden , eller ved at bruge additionen på : .
5. Hvert endeligt tal i har en ``standarddel'':

   

   (Et tal er endeligt, hvis der er med ).

Nu har vi fået infinitessimalerne ind i de reelle tal igen. Det vil sige, vi har fået dem ind i , som nu er vores bud på modellen af de reelle tal. Så er spørgsmålet, om vi har løst de problemer, der var i Leibniz' tid. Lad os se på hvert af de problemer, vi omtalte tidligere:

1. Først var der problemet med differentialkvotienten, hvor vi så på infinitessimaler som værende forskellige fra nul et øjeblik, og lig med nul det næste. Med vores standarddel begreb kan vi hurtigt tage os af dette problem. Vi giver følgende definition af differentialkvotienten af f i x: f'(x) eksisterer, hvis og kun hvis kvotienterne er endelige og uendelig tæt på hinanden for alle infinitessimale værdier . I dette tilfælde er

   

2. Hvad med den Archimediske egenskab, holder den? Svaret på dette spørgsmål er både ja og nej: Achimedes' egenskab kan formuleres som en sætning om superstrukturen .

   

   Leibniz' princip siger nu, at

   

   holder i . Det vil sige, at så længe vi er villige til at tage vore naturlige tal fra (som jo kan være uendelig store), så holder Archimedes' egenskab stadig (og for a og b standard kan man jo selvfølgelig vælge n standard, da sidder inde i med alle dens egenskaber intakte). På den anden side er det da også klart, at hvis , så har vi

   

   Det vil sige, at hvis vi holder os til det metamatematiske begreb af endelighed, så holder Archimedes' egenskab ikke længere. Men den holder nok til, at vi har, hvad vi skal bruge inden for analysen.

3. Og sidst men ikke mindst, hvad kan vi sige om fuldstændigheds-egenskaben? Den holder for de interne delmængder af , men ikke for alle delmængder af . Så her er svaret også både ja og nej. Det, at den holder for interne mængder, er en følge af Leibniz' princip:

   

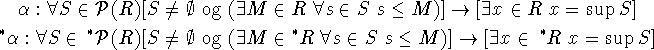
   Argumentet givet tidligere for at vise, at ikke har et supremum holder i , så der er altså ikke-tomme, begrænsede delmængder, for hvilke der ikke findes noget supremum. Vi kan konkludere, at sådanne mængder er eksterne. Så , for eksempel, er en ekstern delmængde af . Dette kan faktisk anvendes til stor fordel, når man skal til at bevise sætninger i analyse (som i `Cauchy-Robinson Overspill Principle' for eksempel), men det får vi desværre ikke plads til at illustrere her.

Til afslutning vil jeg gerne lige illustrere, hvordan dette bruges til at bevise en elementær sætning i reel analyse. Men først begynder vi med en, som du selv kan prøve at bevise (og dermed få lov til at bruge Cauchy-Robinson Overspill principet).

Bevis. Lad K være et uendeligt stor naturligt tal, og del intervallet [a,b] i K lige store dele. Det vil sige, at vi tager

Lad os nu se på mængden . Først skal vi se, at denne mængde er intern:

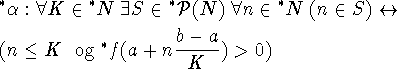
Dette viser, at , så S er intern. Men fra Leibniz' princip ved vi, at dette er sandt for alle ikke-tomme delmængder af . Lad , da har vi og , og selvfølgelig er , da K er uendelig stor. Vi tager nu . Siden f er kontinuert i c, har vi og . Men den eneste måde et standard reelt tal kan være uendeligt tæt på både et positivt og et negativt tal, er hvis tallet selv er nul, det vil sige at f(c)=0.

Kommentarer:

1. Disse metoder blev først udviklet af Abraham Robinson, delvis som svar på Leibniz' ønske om at legitmissere infinitessimalernes tilstædeværelse blandt de reelle tal. Som Robinson selv begyndte at vise i sin bog `Non Standard Analysis', og som også er blevet vist siden da, er disse metoder også meget frugtbare i mange andre områder inden for matematikken.
2. Eksistensen af ikke-standard udvidelser af matematiske strukturer kan ikke påvises konstruktivt. En måde at konstruere disse udvidelser på er ved hjælp af ultraprodukter, og der må vi antage eksistencen af frie ultrafiltre. En anden ting her er, at der selvfølgelig overhovedet ikke er nogen entydighed i ikke-standard udvidelser - der er mange ikke-isomorfe udvidelser.
3. En anden indfaldsvinkel til ikke-standard analyse er gennem en ny aksiomatik for mængdeteorien, som ud over tilhører-prædikatet har et unært prædikat st. Inden for en sådan mængdeteori er der selvfølgelig en entydig konstruktion af de naturlige og de reelle tal - som med det samme vil svare til vore ikke-standard udvidelser. Men man skal ikke lade sig narre, for der er jo mange ikke isomorfe modeller af en mængdeteori, så der er ingen vej uden om at der ikke er nogen entydighed.

Foregående: Matematik på Internet Op: FAMØS december 1996 Næste: Litteratur