Jette Randløv
I denne artikel skal vi se på, hvad postscript er for noget. Mange har måske hørt postscript omtalt som et printersprog udviklet af det amerikanske firma Adobe, hvilket er korrekt. Men postscript er mere end det. Det er også et sprog, hvor man ganske nemt kan tegne og transformere forholdsvis komplicerede geometriske figurer, som ville være særdeles krævende under sædvanlige programmeringssprog som Pascal, C og Fortran. I artiklen skal vi se eksempler på både simple og knap så simple figurer, og hvordan man kan tegne dem vha. postscript. Vi vil også studere lidt af den matematik, postscript bruger til at håndtere kurver og transformationer. Artiklen er ikke en introduktion til programmering i postscript; de vigtigste kommandoer bliver ganske vist forklaret, men postscriptkoden er primært medtaget for at illustrere sprogets simplicitet og for at give læseren et udgangspunkt for selv at prøve.
Postscript adskilder sig fra de fleste programmeringssprog, som er i almindelig brug blandt ikke-dataloger, ved at være et stak-sprog. Tænk på en stak af tal: Man kan lægge nye tal på for oven og tage tal af fra oven, efterhånden som man får brug for dem. En programlinje, der blot består af et tal, lægger dette tal på stakken. En funktion, som skal bruge n variable tager de øverste n variable af stakken og bruger dem.
Betragt for eksempel:
100 50
moveto
I den første linje lægges to tal på stakken, og i den anden tager
funktionen moveto to tal af stakken og bruger dem som x og
y koordinat.
Lad os tage endnu et simpelt eksempel: Hvis stakken er tom, vil 3 4 mul efterlade 12 på stakken som det eneste tal, idet mul er multiplikationsoperatoren.
Lad os springe ud i det med et rigtigt program (se figur 1).
%!PS-Adobe-2.0 EPSF-2.0
%%BoundingBox: -45 -40 30 40
3 { 25 34 moveto
25 -34 lineto
17 -38.2 lineto
17 20 lineto
-17.6 0 lineto
120 rotate
} repeat
stroke
showpage
|
 |
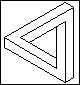Hvad siger koden? Alle linjer, der begynder med ``%'',
opfattes som kommentarer og ignoreres (pånær at den første linje skal
begynde med ``%!'' for at vise, at det er en postscriptfil).
I linjen 25 34 moveto lægges to tal på stakken, og funktionen
moveto fjerner dem igen og flytter til positionen (25,34).
25 -34 lineto tegner en linje til (25,-34) fra den aktuelle
position. Selve stregen bliver dog ikke trukket, men man kan tænke på
det som, at den aktuelle figur tilføjes denne linje. Linjen
120 rotate bevirker, at hele koordinatssytemet bliver rotatet
. Hele tegneprocessen bliver gentaget 3 gange: Tallet i
starten af den tredje linje angiver, hvor mange gange
smørren i de krøllede parenteser gentages. Kontruktionen 3 { ... } repeat i sig selv påvirker ikke stakken. Funktionen
stroke bevirker, at den aktuelle figur bliver tegnet op.
Måleenheden i postscript er typografiske punkter
, som har størrelsen en
-del engelsk tomme, hvilket er ca. 0,0353 cm.
Figur 2 bruger to for-løkker (der gennemløber
tallene 0, 35, ..., 630). Koden til figuren indeholder ud over
for-løkkerne tre nye ting:
%!PS-Adobe-2.0 EPSF-2.0
%%BoundingBox: 0 0 425 630
0.2 setlinewidth
0 35 630 {
0 exch moveto
0 35 630 {
gsave
425 exch lineto stroke
grestore
} for
} for
showpage
Funktionen setlinewidth sætter bredden af linjen, mens
funktionen exch bytter om på de to øverste tal i stakken.
Den grafiske tilstand er en samling af indstillinger og parametre, som
tilsammen beskriver tilstanden af den del af systemet, der vedrører
grafiken, herunder ting som positionen af det aktuelle punkt,
linjetykkelsen, skaleringsgrad, farven eller gråtonen,
rotationsvinklen og den aktuelle transformationsmatrix. Man kan gemme
tilstanden på et bestemt tidspunkt med kommandoen gsave.
grestore genskaber tilstanden som den var ved den tilsvarende
gsave, hvilket ikke nødvendigvis er den sidste, da man kan have
flere niveauer inde i hinanden. I teorien er der ingen grænser for,
hvor mange gsave-grestore sæt, man kan have inde i
hinanden, men i praksis sætter størrelsen af ens printer eller
computers hukommelse en øvre grænse.
I koden til figur 2 gemmes den grafiske tilstand, før en streg tegnes. Dette gøres for at beholde det aktuelle punkt, som ellers ville blive ændret til endepunktet for linjen.
Kochkurven fremkommer ved at tage et linjestykke og finde
`grænsekurven' af følgende proces: I hvert trin erstattes alle
linjestykker med linjestykker, hvor den midterste tredjedel er fjernet og
erstattet af to sider af en ligesidet trekant. Figur
3 viser idéen. Denne fremgangsmåde giver i grænsen
Kochkurven; en fraktal med Hausdorffdimension
.
Figur 3: Kochkurvens kontruktion: Den midterste tredjedel af linjestykket erstattes af to lige så lange linjestykker der udgør to af siderne i en ligesidet trekant.
%!PS-Adobe-2.0 EPSF-2.0
%%BoundingBox: 10 -230 250 80
/funktion {
gsave
.33333333 .33333333 scale
dup
0 gt
{ dup 1 sub
funktion
10 0 rmoveto 60 rotate
funktion
10 0 rmoveto -120 rotate
funktion
10 0 rmoveto 60 rotate
funktion
10 0 rmoveto
pop
}
{ 30 0 rlineto stroke }
ifelse
grestore
} def
26 26 scale 20 setlinewidth
0 0 moveto
0 1 2 {
6 funktion
10 0 rmoveto
-120 rotate
} for
showpage
Figur 4 viser hele Kochkurven med postscriptkoden inde i [kun i papir-udgaven, www-red.]. (Placeringen af koden er ikke en del af programmet.)
Først defineres en funtion funktion, som rekursivt kalder sig
selv. En funktionsdefinition har generelt formen tallet 6 på stakken. Dette tal bestemmer antallet af niveauer i
rekusionen. gt betyder større end, det vil sige, at linjen
0 gt undersøger, om tallet før 0 på stakken er større end 0.
Hvis dette er tilfældet, udføres den første del af ifelse,
ellers den anden del.
Figur 5: Kochkurven med lidt andre parametre til scale: Nedskaleringen med en faktor 
i femte linje af koden er ersattet med linjen 0.4 0.3 scale.
Bézierkurver blev første gang defineret af Pierre Bézier i 1970'erne til CAD/CAM systemer.
En måde at definere kurverne på er følgende:
For en mængde af n+1 kontrolpunkter 
er en
n'te grads Bézierkurve givet som
hvor 
og 
er et Bernstein-polynomium:
Denne definition (den analytiske) siger ikke meget om kurvernes
udseende, når punkterne er givet. Det gør
derimod følgende geometriske definition:
hvor
Idéen er, at man iterativt kan tilnærme sig Bézierkurven ved at betragte konvekse kombinationer af kontrolpunkterne og med konvekse linearkombinationer af de fremkommende punkter osv. Figur 6 viser idéen.
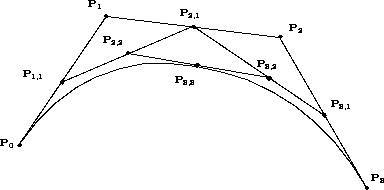
Figur 6: Tredjegrads Bezierkurve med de fire kontrolpunkter og nogle punkter fremkommet som konvekse linearkombinationer.
En Bézierkurve af vilkårlig grad n har visse særlige egenskaber:
og 
ligger på kurven.
.
er linjen mellem og 
,
ligeledes er tangenten i punktet linjen mellem 
og
.
ligger alle på kurven, hvis og kun hvis
den er en ret linje.
Specielt betyder dette, at en tredjegradskurve består af to endepunkter og to punkter, der altid ligger på tangenten til kurven i de to endepunkter.
Tredjegrads Bézierkurver er fundamentale i postscript, og har derfor
deres egen kommando. Hvis man befinder sig i punktet P0 vil
kommandoen P1 P2 P3 curveto give den pågældende Bézierkurve.
Lad os prøve - se figur 7.
%!PS-Adobe-2.0 EPSF-2.0
%%BoundingBox: 10 20 210 170
/P0 { 60 40 } def
/P1 { 200 160 } def
/P2 { 20 100 } def
/P3 { 140 40 } def
P0 moveto
P1 P2 P3 curveto
1.5 setlinewidth
stroke
P0 3 0 360 arc closepath fill
P1 3 0 360 arc closepath fill
P2 3 0 360 arc closepath fill
P3 3 0 360 arc closepath fill
showpage
|
|
Figur 8 illusterer, hvordan flytningen af et kontrolpunkt forandrer kurvens udseende på en intuitiv rimelig måde.
Figur 8: Tredjegrads Bézierkurver med variation af det ene kontrolpunkt.
Den smarte ting ved tredjegrads Bézierkurver er, at de nemt kan
sættes sammen med en 
overgang. For at sikre en kontinuert
overgang mellem to kurver skal man sørge for at første og sidste
kontrolpunkt stemmer. Lad 
være kontrolpunkter for
den første kurve og 
for den anden. Kravet er at
. For at få overgang skal man ydereligere sørge for,
at 
, 
og 
ligger på samme linje.
Lad os prøve at lege lidt med sammensatte Bézierkurver.
Målet er at lave den lange kurve for neden til venstre i figur
9. Denne kurve består af en række ens kurver som er
sammensat med overgang. En af disse kurver er vist i stor udgave
ovenover den lange kurve. Denne kurve er igen sammensat af 4 delkurver
som er ens pånær rotationer og spejlinger. Den første af disse
delkurver kan vi kalde kurve1. En beskrivelse af hele den
lange kurve består således i at beskrive kontrolpunkterne for
kurve1 og rotationerne til dannelse af en enhedskurve og
endelig, hvor mange gange den skal gentages. Dette er faktisk hvad
programmet gør (udover at markere kurve1s kontrolpunkter). De
fire kontrolpunkter er (0,1), , og .
Delkurve nummer 2 (kurve2) fremkommer ved en spejling af
kurve1 gennem den lodrette akse gennem det sidste af
kurve1s kontrolpunkter.
Da vi ønsker -overgange lægger det nogle restiktioner på
ligningerne for kontrolpunkterne. For det første skal kurve1
have en overgang med til en kopi af den selv roteret
grader om kontrolpunktet (0,1). Men en sådan rotation
giver automatisk, at kontrolpunktet og den grader
rotarede udgave ligger på samme linje som rotationspunktet. Det
betyder, at ligegyldigt hvilken værdi har, er -overgangen
sikret. Hvad med den anden ende af kurven? Her er kravet at ,
og punktet, der fremkommer ved en spejling af i den
lodrette akse gennem , skal ligge på en linje. Dette er kun muligt,
hvis og har samme y-koordinat. Disse er derfor begge sat
til 0.
Hele koden til den venstre del af figur 9 (inklusiv indtegning af de fire kontrolpunkter for den første del af kurven) følger her:
%!PS-Adobe-2.0 EPSF-2.0
%%BoundingBox: 108 425 322 662
/vispunkter
{ gsave
0 1 0.03 0 360 arc closepath fill
P1 0.03 0 360 arc closepath fill
P2 0.03 0 360 arc closepath fill
s 0 0.03 0 360 arc closepath fill
grestore
} def
/spejl % (x,y) --> (x+2(s-x),y)
{ exch dup s exch sub 2 mul add exch } def
/grundkurve
{ 4 s mul 0 translate
gsave
newpath
kurve1 kurve2
currentpoint 2 mul exch 2 mul exch translate
180 rotate
kurve2 kurve1
grestore
} def
/P1 { 0.44 0.5 } def
/P2 { 0.35 0 } def
/s 0.13 def % P3 = (s,0)
/kurve1
{ 0 1 moveto
P1 P2 s 0 curveto
gsave stroke grestore
} def
/kurve2
{ s 0 spejl moveto
P2 spejl P1 spejl 0 1 spejl curveto
gsave stroke grestore
} def
gsave
150 500 translate 80 80 scale
0.015 setlinewidth
grundkurve
vispunkter
grestore
gsave
100 430 translate 20 20 scale
0.03 setlinewidth
20 { grundkurve } repeat
grestore
stroke
showpage
Den højre del af figur 9 er fremkommet ud fra den
venstre ved at tilføje en tykkelse til linjerne. Men i stedet for blot
at bruge scale og setlinewidth, er `linjens' omkreds
tegnet og resulatet er derefter udfyldt med sort. Denne omkreds fundet
ved at forskyde kontrolpunkterne og en smule og bruge den
resulterende Bézierkurve til at danne en lukket kurve.
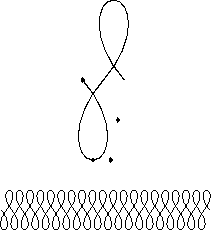
Figur 9: Til højre er den samme krusedulle som til venstre, men tilføjet vægt og stabilitet ved at gøre en del af kurven tykkere.
Før vi ser nærmere på skriftsnit og deres forbindelse til postscript, er her et lille eksperiment til at undersøge, hvor meget vi egentlig lægger mærke til skriftsnittene.
Times Roman skriftsnittet er formentlig et af de mest brugte skriftsnit i de seneste 100 år i lande med latinsk alfabet. Times Roman bliver brugt i mange bøger, aviser, tryksager og tekstbehandlingsprogramer. Mange mennesker betragter Times Roman som en inkarnation af, hvordan de latiske bogstaver `virkelig' ser ud. Det er formentlig rimeligt at gætte på, at læseren på nuværende tidspunkt har set et Times Roman bogstav over 1 million gange.
Lad os derfor prøve følgende lille øvelse. Luk FAMØS og tegn et lille ``l'' og et lille ``g'' af Times skrifttypen. Læs ikke videre, før du har prøvet!
En figur med de to bogstaver i Times Roman findes til slut i artiklen
på side 
.
Af disse seks spørgsmål er det kun de sidste to, der faktisk er svære, blandt andet fordi forskellige skriftsnit, der ser `almindelige' ud er forskellige på disse punkter. Alligevel kræver det et ualmindeligt skapt øje for detaljer at svare rigtigt på mere end to af spørgsmålene, hvis man ikke haft noget med skriftsnit af gøre før.
Det er ganske almindeligt ikke at bemærke bogstavernes tykkelse og særligt deres varierede tykkelse. Generelt mener de fleste, at et skriftsnit med betoning af streger, der går fra øverst til venstre til nederst til højre er mere rolig og behagelig at læse - pudsigt nok samtidig med at de fleste ikke bemærker forskellen i tykkelse. Baggrunden for at netop disse streger betones, er et levn helt tilbage fra bogstaverne form blev defineret udelukkende gennem håndskrift [1].
I den venstre del af figur 9 var vægten da netop også føjet til de linjer, man naturligt ville betone hvis man skulle tegne kurven i hånden. Læseren kan forvisse sig om, at en tilsvarende effekt ikke indtræffer ved modsat betoning, ved at holde kurven op foran et spejl.
Hvad har skriftsnit og postscript overhovedet med hinanden at gøre? En hel del faktisk. Adobe udviklede oprindeligt postscript netop for at have et sprog til at definere skriftsnit i.
Det enkelte bogstav bliver defineret ved at give kurven `rundt om' bogstavet og derpå fylde det indre ud med sort. Nedenfor er kurven tegnet op fremfor at fylde den ud:
%!PS-Adobe-2.0 EPSF-2.0 %%BoundingBox: 0 0 430 60 0 15 moveto 0.2 setlinewidth /ZapfChancery-MediumItalic findfont 60 scalefont setfont (Matematik er sundt) true charpath stroke showpage``ZapfChancery-MediumItalic'' er navnet på skriftsnittet og de 60 er størrelsen i punkter.
charpath tager kurvestykkerne fra
bogstaverne og lægger dem til i forlængelse af den aktive kurve (som i
dette eksempel er tom). Endelig tegnes kurven på normal
vis.
ZapfChancery skriftsnittet blev oprindeligt designet af Herman
Zapf. Blandt almindelige skriftsnit-brugere (som vi jo
alle er) er han mere kendt for skriftsnittet ZapfDingbats (her er et
udvalg):
Zapf har designet en del andre skriftsnit, særlig kendt er Palatino og Optima, som bruges i bogtrykning. (Overskriften til denne artikel er sat med Palatino-Bold - skyggerne er ikke inklusiv). For nyligt fik han af American Mathematical Society den opgave at designe et skriftsnit udelukkende med henblik på sætning af matematik. Den nye familie af skriftsnit, der går under navnet AMS Euler (se figure 10), er kendetegnet ved deres `håndskrevne' stil. Idéen er, at de skal se ud som om, de var skrevet af en matematiker med en fremragende håndskrift. Contrete Mathematics [2], som er blevet anvendt på Mat X, brugte denne familie til matematikken.
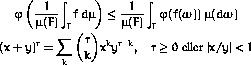
Figur 10: Jensens ulighed og binomialformlen sat med Herman Zapfs skrifttype AMS Euler.
Skriftsnittenes geomtriske defintion gør det særlig nemt at manipulere med dem på forskellig vis. Til formålet findes der en transformationsmatrix.
%!PS-Adobe-2.0 EPSF-2.0 %%BoundingBox: 0 0 330 80 0 40 moveto /Helvetica-Bold findfont 50 scalefont setfont gsave [ 1 0 2 -1 0 0 ] concat 0.6 setgray (L) show /ae glyphshow (s Fam) show /oslash glyphshow (s) show grestore (L) show /ae glyphshow (s Fam) show /oslash glyphshow (s) show showpage
Som det ses krævede de to danske tegn lidt krumspring.
Linjen [ 1 0 2 -1 0 0 ] concat angiver og aktiverer en
transformationsmatrix. Hvad er nu det for en størrelse? I planen kan
en hver skalering og rotation udtrykkes med en 
-matrix.
Vi er imidlertid interesseret i også at udtrykke translation, altså:
eller
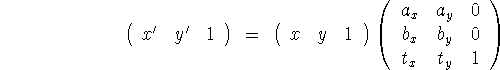
I postscript angiver man transformationsmatricen som en vektor på
formen 
.
En matrix som 
svarer
således til 2 3 scale. 
translaterer efter vektoren 
. Det er ikke
vanskeligt at regne ud hvad matricen i programmet gør. Ganger man ud,
får man transformationen 
.
Figur 11: Et gråtone-billede hevet først gennem en transformationsmatrix [0.8 0 0.6 1 1.2 0] og dernæst igennem [0.7 1.3 -0.2 1 2 -1].
Figur 11 viser transformationsmatricen anvendt på et gråtone-billede. Neutzsky-Wulffs bog Postscript-programmering [6] giver flere eksempler på den slags anvelser (men han påtager sig tilgengæld intet ansvar for om læserne får nervesammenbrud af sidde og tælle raster med en lup for at skrive et gråtonebillede i postscriptkode...)
Er det så tilfældet, at man starter ud med en `nulstillet'
transformationsmatrix? Faktisk ikke, men det er nyttigt at tænke på
det sådan. Hemmeligheden er, at der sker visse
postscriptfortolker-afhængige transformationer undervejs, men hvis
man tager dem i betragtning i koden, bliver koden
hardwareafhængig.
Postscript bliver brugt rigtig meget. Mange progammer, der på en eller
anden måde resulterer i, at noget skrives ud på en printer, konverterer
tekst og grafik til postscriptkode. Læseren kender nok allerede til
dette fra dvips.
Ud over den indirekte brug af postscript vil de fleste vil nok have størst glæde af sproget til at skrive illustrationer til artikler og opgaver i. Ganske vist findes der udemærkede programmer til at tegne illustrationer i, men mange figurer er meget hurtigere at skrive som et program end at tegne.
Inden for mange felter i videnskab (desværre endnu ikke så meget indenfor matematik) er et stort antal af videnskabelige artikler tilgængelige på Internet. Til tider er det netop via Internet, man ser en artikel første gang - måneder før den bliver trykt. Ofte har man behov for at citere en illustration fra en artikel. Mange udskriver derfor artiklen og indskanner derpå illustrationen. Men hvis man allerede har artiklen elektronisk (hvilket stort set altid betyder i postscriptformat) er det meget hurtigere at tage den relevante postscriptkode ud og bruge den direkte.
Skulle læseren have fået lyst til at se nærmere på postscript vil nogle praktiske bemærkninger formentlig være nyttige.
For at se resulatet af koden skal man have fat i en postscriptfortolker. En vilkårlig postscriptprinter kan bruges til dette formål. På en UNIX-maskine skulle kommandoen ``lpr filnavn'' gerne resulterer i at mesterværket kommer ud af printeren. Programmer som ghostview og ghostscript, som findes til alle operativsystmer, er ligeledes postscriptfortolkere.
Postscriptkode indledes altid med ``%!'' - også selvom ``%'' normalt betegner en kommentar - for at for eksempel en printer kan vide, at filen skal opfattes som postscript og ikke som en almindelig tekstfil.
Husk kommandoen showpage til sidst på en postscript side -
ellers forbliver den blank.
Figurerne vist i denne artikel er generelt mindre end den tilhørende
kode forskriver, idet FAMØS under trykningen bliver forstørret ned
med end faktor 
.
Bemærk, at de skrifttyper, man ser på skærmen, ikke altid er helt de
samme som dem, der bliver benyttet i postscriptprintere. Times Roman
f.eks. er beskyttet af copyright, så hvis man bruger et program som
ghostscript til at se en postscriptfil, der bruger Times Roman, ser
man kun en skrift, der ligner.
Figur 12: Times-Roman. Størrelsen er 90 punkter.