Niels Hansen
Jeg vil i denne artikel præsentere en, synes jeg, meget interessant
sætning, der går under navnet Riesz' repræsentationssætning. Med
den i hånden er det relativt nemt at indføre Lebesguemålet på
![]() såvel som på
såvel som på ![]() . Metoden er væsentlig
forskellig fra den klassiske indførelse, der optræder (delvist) på
3MI. Her konstrueres Lebesguemålet m udfra ønsket om, at m([a,b])
= b - a hvor
. Metoden er væsentlig
forskellig fra den klassiske indførelse, der optræder (delvist) på
3MI. Her konstrueres Lebesguemålet m udfra ønsket om, at m([a,b])
= b - a hvor ![]() og
og ![]() . Konstruktionen ved
hjælp af Riesz' repræsentationssætning bygger derimod på, at
Lebesgueintegralet (integralet mht. Lebesguemålet) skal være en
udvidelse af Riemannintegralet.
. Konstruktionen ved
hjælp af Riesz' repræsentationssætning bygger derimod på, at
Lebesgueintegralet (integralet mht. Lebesguemålet) skal være en
udvidelse af Riemannintegralet.
Det er nok allerede gået op for læseren, at artiklen baserer sig på kendskab til 3MI eller tilsvarende kurser, men med 3MI og 2AN i baglommen, skulle man være på banen. Vi får dog også brug for lidt topologi, men det er mest for at formulere repræsentationssætningen så generelt som muligt. Er man ikke inde i topologi, så går man ikke helt galt i byen, hvis man blot tænker på metriske rum.
Lad nu ![]() være et topologisk rum. Vi skal først indføre et par
nødvendige begreber vedrørende topologien på X.
være et topologisk rum. Vi skal først indføre et par
nødvendige begreber vedrørende topologien på X.
![]() er et lokalkompakt metrisk rum (med den sædvanlige
metrik). Vi har jo, at de kompakte mængder i
er et lokalkompakt metrisk rum (med den sædvanlige
metrik). Vi har jo, at de kompakte mængder i ![]() netop er de
afsluttede og begrænsede mængder.
netop er de
afsluttede og begrænsede mængder.
Vi betragter fra nu af et lokalkompakt Hausdorff topologisk rum ![]() . I resten af artiklen vil
. I resten af artiklen vil ![]() stå for
Borel-
stå for
Borel- ![]() -algebraen på X, dvs.
-algebraen på X, dvs. ![]() er den mindste
er den mindste
![]() -algebra, der indeholder de åbne mængder. Et mål på
-algebra, der indeholder de åbne mængder. Et mål på
![]() kaldes et Borelmål.
kaldes et Borelmål.
For den slags mål findes et par betegnelser, der angiver hvor
``regulært'' målet er. Dermed menes i en eller anden forstand hvor
pænt målet er. Lad nu ![]() være et vilkårligt Borelmål.
være et vilkårligt Borelmål.
![]()
Hvis alle Borelmængder er ydre regulære, siger vi, at ![]() er ydre
regulært.
er ydre
regulært.
![]()
Hvis alle Borelmængder er indre regulære, siger vi, at ![]() er
indre regulært.
er
indre regulært.
Vi erindrer fra 3MI/2MA (eller ser nu for første gang), at et Borelmål
![]() på
på ![]() kaldes et Radonmål, hvis det opfylder
kaldes et Radonmål, hvis det opfylder
![]()
Pointen er, at ![]() er så pænt et rum, at alle Radonmål bliver
regulære, og således forsvinder regularitetsproblemer for Borelmål
på
er så pænt et rum, at alle Radonmål bliver
regulære, og således forsvinder regularitetsproblemer for Borelmål
på ![]() , blot (*) er opfyldt. (Man kan evt. løse opgave 5.16
og 5.17 i 2MA-noterne bind II B).
, blot (*) er opfyldt. (Man kan evt. løse opgave 5.16
og 5.17 i 2MA-noterne bind II B).
Støtten for en funktion ![]() defineres som
defineres som
![]()
Mængden af kontinuerte funktioner fra X ind i ![]() med
kompakt støtte betegnes
med
kompakt støtte betegnes ![]() . Man overbeviser sig let om, at
. Man overbeviser sig let om, at
![]() er et vektorrum med sædvanlig punktvis addition og skalar
multiplikation.
er et vektorrum med sædvanlig punktvis addition og skalar
multiplikation.
Vi kan således nu betragte de lineære funktionaler ![]() . En lineær funktional I kaldes positiv såfremt
. En lineær funktional I kaldes positiv såfremt
![]() hvis
hvis ![]() (
( ![]() ).
).
Endelig kan vi formulere Riesz' repræsentationssætning. Der mindes om, at et mål kaldes fuldstændigt, såfremt alle nulmængder er målelige.
Lad ![]() være et lokalkompakt
Hausdorff topologisk rum og I en positiv lineær funktional på
være et lokalkompakt
Hausdorff topologisk rum og I en positiv lineær funktional på
![]() . Da findes en
. Da findes en ![]() -algebra
-algebra ![]() og netop et fuldstændigt mål
og netop et fuldstændigt mål ![]() på
på ![]() så
så
![]()
Det er selvfølgelig punkt 4, der er af særlig interesse.
Jeg har ikke tænkt mig at gengive beviset her, da det er relativt langt (ca. 6 sider), og kræver visse topologiske resultater. Jeg må derfor henvise til [1] for beviset.
Der er visse problemer, om man vil, med regulariteten af målet, men
det kan der altså ikke gøres noget ved i den generelle situation. En
forudsætning om at X er ![]() -kompakt (X er en tællelig
forening af kompakte mængder) vil dog sikre, at målet bliver regulært,
men igen vil jeg henvise til [1] for bevis.
-kompakt (X er en tællelig
forening af kompakte mængder) vil dog sikre, at målet bliver regulært,
men igen vil jeg henvise til [1] for bevis.
Lad ![]() og betragt følgende
afbildning
og betragt følgende
afbildning ![]() givet
ved
givet
ved ![]() , der er kendt som Diracs delta-funktion.
Denne er klart en positiv lineær funktional, så ifølge sætning 1.a
findes en
, der er kendt som Diracs delta-funktion.
Denne er klart en positiv lineær funktional, så ifølge sætning 1.a
findes en ![]() -algebra
-algebra ![]() , og
et mål
, og
et mål ![]() , så for
, så for ![]() er
er
![]()
Det er ikke svært at se, ved hjælp af Lebesgues sætning om
majoriseret konvergens, at ![]() er etpunktsmålet i x. Dvs.
målet er for
er etpunktsmålet i x. Dvs.
målet er for ![]() givet ved
givet ved
![]()
Dette mål går også under navnet Dirac målet i x.
Vi kunne nu indføre Lebesguemålet ligesådan ved hjælp af sætning 1.a, men jeg har valgt at gå en lille omvej.
![]()
Da ![]() er et lokalkompakt Hausdorff topologisk rum følger
eksistensen af sætning 1.a ved restriktion af det der givne mål
er et lokalkompakt Hausdorff topologisk rum følger
eksistensen af sætning 1.a ved restriktion af det der givne mål
![]() til Borel-algebraen (vi
sætter
til Borel-algebraen (vi
sætter ![]() . Vi har jo, at for
. Vi har jo, at for ![]() findes en følge af simple Borelfunktioner, der
konvergerer mod f majoriseret af |f|. Da integralet af de simple
Borelfunktioner er det samme, uanset om vi integrerer mht.
findes en følge af simple Borelfunktioner, der
konvergerer mod f majoriseret af |f|. Da integralet af de simple
Borelfunktioner er det samme, uanset om vi integrerer mht. ![]() eller
eller ![]() , da følger det af Lebesgues majorantsætning, at
integralet mht.
, da følger det af Lebesgues majorantsætning, at
integralet mht. ![]() repræsenterer I.
repræsenterer I.
Jeg vil vise entydigheden direkte, men for at gøre det skal vi bruge et lille lemma. Først erindres dog om Urysohns lemma for metriske rum (opgave I.3.7 fra 2AN).
Lad (M,d) være et metrisk rum, og lad ![]() og
og ![]() være to
afsluttede disjunkte delmængder af M. Der findes en kontinuert
funktion
være to
afsluttede disjunkte delmængder af M. Der findes en kontinuert
funktion ![]() så f(x) = 0 for
så f(x) = 0 for ![]() og
f(x) = 1 for
og
f(x) = 1 for ![]() .
.
Lad K og V være hhv. en kompakt
delmængde og en åben delmængde af ![]() , således at
, således at ![]() . Da findes en funktion
. Da findes en funktion ![]() , hvor
, hvor
![]() for alle
for alle ![]() , f(x) = 1 for
, f(x) = 1 for
![]() , og
, og ![]() .
.
Da ![]() og V er åben, vil der for
alle
og V er åben, vil der for
alle ![]() findes et
findes et ![]() , så
, så ![]() . Vi kan endog vælge
. Vi kan endog vælge ![]() så lille, at
så lille, at
![]() . Vi har at
. Vi har at
![]()
så da K var kompakt, kan denne åbne overdækning udtyndes til en
endelig. Dvs. der findes ![]() , så
, så

Sæt nu ![]() , så vil
, så vil ![]() . Ifølge Lemma 2 er der
en kontinuert funktion
. Ifølge Lemma 2 er der
en kontinuert funktion ![]() , så f
er 1 på K og 0 på
, så f
er 1 på K og 0 på ![]() . Dette giver at
. Dette giver at ![]() , så
, så ![]() , hvilket viser at
, hvilket viser at ![]() , og
da
, og
da ![]() er kompakt, at
er kompakt, at ![]() .
.
Funktionen i lemmaet opfylder altså uligheden ![]() .
.
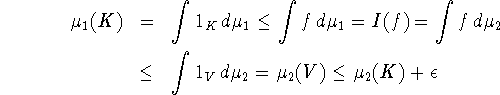
Da ![]() var vilkårlig, slutter vi at
var vilkårlig, slutter vi at ![]() .
Af symmetrigrunde er
.
Af symmetrigrunde er ![]() , så
, så ![]() for alle kompakte delmængder
for alle kompakte delmængder ![]() .
.
Pointen er, at ovenstående entydighedsbevis kan kopieres til det generelle tilfælde, hvis man altså kan bevise lemma 3. I sætning 1.a er målet godt nok ikke regulært, men er stadig bestemt af målet på de kompakte mængder.
Lemma 3 kan vises generelt, altså for lokalkompakte Hausdorff topologiske rum, men det er ganske bemærkelsesværdigt, at lemma 2 ikke gælder generelt for disse rum, så beviset bliver nødvendigvis en del anderledes.
Det står nu klart, at entydigheden i sætning 1.a er relativt let
klaret, og tilbage står problemet med selve konstruktionen af målet.
Det vil vi ikke bekymre os om, men derimod benytte sætningen til
konstruktion af Lebesguemålet på ![]() .
.
Vi betragter nu den positive lineære funktional ![]() for
for ![]() . Integralet er
her Riemannintegralet af f over hele den reelle akse, hvilket giver
god mening, da f er 0 udenfor et kompakt interval [a,b] og f
er kontinuert.
. Integralet er
her Riemannintegralet af f over hele den reelle akse, hvilket giver
god mening, da f er 0 udenfor et kompakt interval [a,b] og f
er kontinuert.
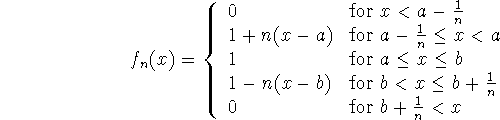
Da vil ![]() majoriseret af den
integrable funktion
majoriseret af den
integrable funktion ![]() , så da
, så da ![]() følger af Lebesgues majorantsætning at
følger af Lebesgues majorantsætning at
![]()
men da ![]() slutter vi at m([a,b])=b -
a.
slutter vi at m([a,b])=b -
a.
Det er nok en god ide, om man tegner funktionen ![]() . Mht.\
entydighed af Lebesgue målet, så giver sætning 1.b os, at der ikke
findes andre Radonmål, der repræsenterer Riemannintegralet, men vi
får ikke umiddelbart, at målet m er entydigt blot m([a,b]) = b -
a. Dette vises dog på 3MI. Det i sætning 2 angivne mål m vil vi
kalde Lebesguemålet på
. Mht.\
entydighed af Lebesgue målet, så giver sætning 1.b os, at der ikke
findes andre Radonmål, der repræsenterer Riemannintegralet, men vi
får ikke umiddelbart, at målet m er entydigt blot m([a,b]) = b -
a. Dette vises dog på 3MI. Det i sætning 2 angivne mål m vil vi
kalde Lebesguemålet på ![]() , defineret på Borelalgebraen.
Havde vi indført målet ved hjælp af sætning 1.a i stedet, havde vi
fået en større
, defineret på Borelalgebraen.
Havde vi indført målet ved hjælp af sætning 1.a i stedet, havde vi
fået en større ![]() -algebra, der normalt kaldes Lebesguealgebraen,
og målet kaldes det fuldstændige Lebesguemål. På
-algebra, der normalt kaldes Lebesguealgebraen,
og målet kaldes det fuldstændige Lebesguemål. På
![]() kan Lebesguemålet indføres ligesådan, men der bliver
en anelse flere tekniske detaljer.
kan Lebesguemålet indføres ligesådan, men der bliver
en anelse flere tekniske detaljer.
Ligeså nemt viser man, at hvis ![]() er en
kontinuert funktion, og man sætter
er en
kontinuert funktion, og man sætter
![]()
Da er
![]()
hvor der på venstresiden står Riemannintegralet og på højresiden Lebesgueintegralet mht. Lebesguemålet m. Man benytter blot en konstruktion tilsvarende den i beviset for sætning 2 og med sætningen om majoriseret konvergens følger resultatet (*).
Jeg håber at læseren er kommet så vidt, at han/hun læser denne linie. Ønsker man at studere emnet nøjere på egen hånd, så kan jeg først og fremmest henvise til [1], der er en rigtig god analysebog. Man kan også gribe fat i [2] (kapitel 6), der (med forfatterens egne ord) er en ``high tech'' introduktion til emnet. God fornøjelse med videre studier!