Henrik Chr. Grove
I sidste nummer stillede vi en opgave der gik ud på at bestemme sandsynligheden P(N,K) for, at man med N snit kunne få skåret K kartofler i stykker, med en lidt urealistisk fremgangsmåde.
Det er vel klart for de fleste, at den valgte fremgangsmåde, giver en ganske stort antal mulige forløb, bare med to kartofler er der efter to snit, to muligheder for hvad man har lignende i gryden, nemlig enten 4 halve, eller en hel, en halv og to kvarte kartofler.
Når man har gjort sig dette klart, finder man let ud af at antallet af kartoffelstykker i gryden ikke kan bruges til noget. Man er nødt til at kigge på flere variable end de to nævnte. Kald antallet af halve kartofler i gryden for H, og antallet af stykker der maksimalt er en fjerdedel for M. Lad S være det samlede antal katoflerstykker i gryden, altså S = K+H+M.
Definér:
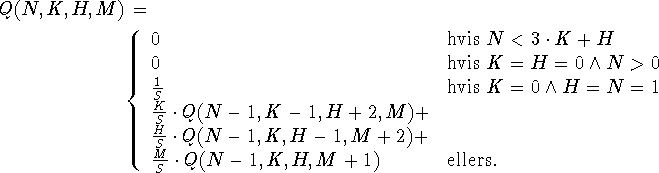
Så er P(N,K) = Q(N,K,0,0).
Det er ikke så svært at se at funktionen Q(N,K,H,M) faktisk løser
opgaven. Første linie siger, at der skal bruges mindst 3 snit pr. hel
kartoffel, plus et pr. halve. Anden linie siger, at vi ikke kan bruge
ét eneste snit mere, hvis
vi er færdige. Tredje linie siger, at hvis der er netop én halv kartoffel
tilbage, og vi vil bruge netop ét snit, har vi en sandsynlighed på
, for at det lykkes os at blive færdige, dette er netop
sandsynligheden for, at vi vælger den halve kartoffel. De sidste tre linier
siger, at ellers vil vi tage et stykke af en given størrelse, med en
sandsynlighed, på antallet af stykker af den størrelse divideret med antallet
af stykker i alt. Dette stykke skærer vi over, og gentager derefter processen
til vi havner i et af de første tre tilfælde.
Jeg påstod som et ,,vink'' til opgaven, at de urealistiske antagelser ikke gjorde opgaven sværere, det kan selvfølgelig diskuteres, men den her fundne løsning, kan hurtigt ændres så den passer på nogle mere realistiske antagelser. Hvis man f.eks. ikke har lyst til at risikere at skulle spalte atomer, kan man bare ændre M+1 til M i den sidste linie af formlen. Hvis man mener at sandsynligheden for at vælge et stykke kartoffel, er proportionalt med dets størrelse, skal man bare ændre lidt på brøkerne i de 4 sidste linier.