Christian Ivar Westergaard
Figur 1: Hieronymus Georg Zeuthen (1839-1920)
Hieronymus Georg Zeuthen (figur 1) fødtes 15. februar 1839 i Grimstrup ved Varde og var søn af F. L. B. Zeuthen som tilhørte en af vort lands ældste præsteslægter, hvoraf det flotte fornavn stammer. Fra hjemmet fik han sin første undervisning, og en interesse for det religiøse og åndelige fulgte ham gennem hele livet. Da faderen blev forflyttet til Sorø, begyndte sønnen som 10-årig i denne lærde skole. Her mødte han sin senere kollega Julius Petersen. Allerede på dette tidspunkt begyndte en kappestrid om, hvem af dem der kunne komme videst omkring i matematiken. Senere sagde Zeuthen, at kappestriden var en væsentlig spore til arbejdets fremme.
I 1857 dimitterede Zeuthen fra Sorø og begyndte året efter både at følge forelæsninger på Polyteknisk Læreanstalt og ved Universitet. Undertiden var det matematikerne Chasles' og Salmons nyere arbejde over geometrien, som medrev Zeuthen og det kan vel siges dette var indgangen til det ene af de to emner som han mesterligt beherskede, nemlig Antalgeometrien og Matematikens historie.
Som 23-årig blev Zeuthen magister og rejste på stipendium til Paris for at studere videre hos antalgeometriens grundlægger Chasles. Studiet blev dog afbrudt af krigen, men efter at have aftjent sin værnepligt som officeraspirant i artilleriet, vendte Zeuthen tilbage til Paris og fik nu rig lejlighed til at udforme sin doktordiputats om karakteristikerne ved systemer af keglesnit. Dette var et emne som Chasles havde opfordret Zeuthen til at undersøge, og sidst i 1865 forsvarede Zeuthen ``Nyt Bidrag til Læren om Systemer af Keglesnit, der er underkastede fire Betingelser''. Disputatsen vandt usædvanlig stor anerkendelse og blev hurtigt oversat i Nouvelles Annales. Dette emne kan kort siges at beskæftige sig med antallet af løsninger til en algebraisk-geometrisk opgave. Som Zeuthen selv indleder med, er dette i mange tilfælde en videre anvisning til selve opgavens løsning. Er man f.eks. kommet frem til at der er 6 keglesnit, som går gennem fire givne punkter og rører et givet keglesnit, kan dette benyttes til at finde selve disse keglesnit.
Røringspunktet P og det keglesnit som de alle rører, K, og et af de søgte keglenit vil nemlig have samme polar med hensyn til K og med hensyn til et keglesnit gennem de fire givne punkter.
Stedet for et punkt, der har samme polar med hensyn til K og med hensyn til et keglesnit gennem de fire punkter, vil altså skære K i 6 punkter, og derfor være af 3. grad. Men af denne kurve kan man derefter let finde så mange punkter, man vil, og derved bestemme kurven, hvorved opgaven betragtes som løst.
Det var Chasles som indførte de vigtige karakteristikker 
og
i systemer af keglesnit, der var underkastet visse
betingelser. Her er antallet af de keglesnit i systemmet, der
går gennem et vilkårligt forelagt punkt, og antallet af
keglesnit, der rører en vilkårlig forelagt linie. Zeuthens nye bidrag lå i
at forbinde disse karakteristikker med 
og 
, som
henholdsvis er antallet af liniepar (udartede punktløb) og antallet af
punktpar (udartede linieløb). Disse forbinder Zeuthen ved hjælp af det
Chasles'ske korrespondanceprincip;
hvoraf nu også og kan findes
Endnu inden disputatsen var antaget, læste Zeuthen i Comptes Rendus, at Chasles havde bebudet en undersøgelse af karakteristikkerne for systemer af flader af 2. orden, altså en almindeliggørelse af opgaven om keglesnit. Zeuthen var klar over at han med lethed kunne overføre sine metoder om keglesnit til flader. Zeuthen indleverede en forseglet konvolut til Videnskabernes Selskabs Skrifter med anmodning om først at åbne kuverten efter Chasles' arbejde var blevet offentliggjort, dels for at vise sin ærbødighed over for Chasles og dels at vise, at det var Chasles, der havde ledt ham ind på emnet.
Nu fulgte en lang række arbejder over dette emne, som både udkom i Videnskabernes Selkabs Skrifter og Mathematisk Tidsskrift, som han selv fra 1870 og 19 år frem var udgiver af. Zeuthens bidrag til dette tidsskrift var enormt, og rundt omkring i verden var det kendt som Zeuthens Tidsskrift. Det hele kulminerede i det store værk Almindelige Egenskaber ved Systemer af plane Kurver med Anvendelse til Bestemmelse af Karakteristikkerne i de elementære Systemer af fjerde Orden. Gennemførelsen af dette meget omfattende arbejde vidner ikke blot om en overlegen geometrisk intuition, men også om en utrolig energi. Eksempelvis skal nævnes, at antallet af algebraiske kurver af 4. orden, der rører 13 givne linier og går gennem et givet punkt er 2.301.119.144.
Zeuthens allerbetydeligste præstationer i den algebraiske geometri var Undersøgelser over Transformationer af Kurver og Flader. Først den almindelige slægtsætning, der forud var kendt, men som Zeuthen på en særlig simpel måde drog ind under sine metoder:
Fra 2 punkter 
og 
projiceres tilsvarende punkter
og 
, der gennemløber to kurver 
og 
, ved
to liniebundter 
og 
, der ved skæring
mellem tilsvarende stråler i 
frembringer en ny kurve
. Den søgte antalrelation findes nu ganske simpelt ved at
udtrykke, at antallene af tangenter fra og til denne
kurve er lige store. Det gælder blot om at tælle rigtigt dvs. i
overenstemmelse med de algebraiske dannelsers væsen, og dette var for
Zeuthen den egentlige opgave.
Zeuthen udvidede straks sin metode til flertydige korrespondancer, og
fandt derved den udvidede slægtsætning, la formola di Zeuthen,
som italienerne kaldte den.
Omkring 1880 blev Zeuthens interesser draget mere og mere over imod matematikens historie. Zeuthen havde et nært samarbejde med Heiberg, som var indledt ved dennes doktordisputats, Quaestiones Archimedeae, der var skrevet på latin, hvortil Zeuthen meldte sig som opponent. Dette samarbejde, som blev fortsat gennem årene, bidrog i høj grad til, at Zeuthen med stor kraft satte ind også på det matematikhistoriske område.
I 1885 udkom hans store værk i Videnskabernes Selskabs
Skrifter: Keglesnitslæren i Oldtiden, der på én gang gjorde
Zeuthen berømt også som historiker. Her indleder han med at omtale
Descartes, som siger, at de gamle grækere ikke havde nogen virkelig metode
(den analytiske geometri) til at finde alle sætninger, men at de blot
samlede dem, som de tilfældigvis stødte på. Zeuthen viser i sit værk
særlig at Apollonius i sin Keglesnitslære benyttede sig af de samme
metoder som vi gør nu til dags, men blot udtrykt i et andet sprog, nemlig den
geometriske algebra. Eksempelvis accepterer vi den moderne formel om en
sums kvadrat 
hvorimod grækerne konstruerede denne størrelse, og
dermed bekræftede dens eksistens, ved figuren
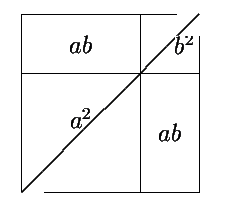
som udsiger, at ``et Rektangel, hvis Sider selv ere Summer, bliver Summen af alle de Rektangler, som til Sider have et Led i hver af de givne Summer''.
Med denne metode kunne de også finde de positive rødder i kvadratiske ligninger som
ved geometriske kontruktions-opgaver. Nemlig at finde siden x
således at differensen mellem et rektangel med arealet ax og
kvadratet med arealet 
bliver et areal på 
.
I 1893 udkommer første bind af hans verdenskendte Forelæsning over Mathematikens Historie. Oldtid og Middelalder. og i 1903 andet bind om det sekstende og syttende århundrede. Værket blev senere oversat til tysk og er nok det de fleste forbinder Zeuthen med. Det var i dette værk, Zeuthen siger at i oldtiden var konstruktionen eksistensbevis. Når Euclid i sin første bogs første sætninger lærer at kontruere en ligesidet trekant, er det ikke for at gøre opmærksom på, at en sådan kan man konstruere, når man har lineal og passer ved hånden, men for at sikre at en sådan trekant eksisterer.
Den nye opfattelse forklarer også, hvorfor Apollonius begyndte sin
keglesnitslære med at opfatte kurverne som snit i cirkulære
kegler. Nu ser man, at det var for at sikre sig kurvernes eksistens
som sådanne, idet cirklens eksistens for Euclid er aksiomatisk
givet. Man ser, at Zeuthen stadig vender tilbage til sine opgaver for at
komme dybere ind på dem. Der er særlig et punkt, hvor betydningen af
Zeuthens opfattelse er væsentlig, nemlig ved forståelsen af
parallelaksiomet. Dette kaldtes i tidligere tid for det XI aksiom, men
blev kendt som det 5te postulat. Men først Zeuthens bemærkning gav den rent
matematiske forklaring heraf. Parallelaksiomet er et eksistensaksiom
ligesom de øvrige postulater.
Ved tiden hen imod slutningen af det forrige århundrede begynder den
tredie, den sidste og lange periode af Zeuthens liv. Nu følger en uafbrudt
række af systematiske og historiske arbejder skiftevis efter hinanden,
og der sker noget nyt ved Zeuthens stil som ellers før var uforligneligt
``lærd'', præcis og knudret, men nu bliver den mere letflydende og populær.
Zeuthen fortæller selv om, hvor stort
et arbejde han satte ind på at erhverve sig personlig færdighed i
brugen af de gamles geometriske algebra, og han hævder med styrke, at
denne geometriske algebra, som stadig arbejder med figurerne, ikke står
tilbage for nutidens algebra med de mere abstrakte bogstavsymboler,
sålænge der kun var tale om mundtlig fremstilling, hvor man havde
figurerne at pege på.
Om sin historieskrivning siger Zeuthen selv:
``Til at nå dette mål kræves først og fremmest studium af de betydeligste gamle forfattere, og et studium, som ikke går ud fra, at vor tid er blevet klogere end de var, men går ud på at lære noget af dem, navnlig at få fat på det i deres synsmåder, som måtet være gået tabt under den senere generaliserende udvikling.''
Efter tidligere at være trængt dybt ind i oldtidens matematiske viden fra dens guldalder, søger Zeuthen i sine sidste arbejder længere tilbage, til det naturlige og ligefremme grundlag, som må gå forud for enhver formel opbygning af en videnskab. Og ad den vej er han kommen til også at interessere sig for de moderne undersøgelser over geometriens grundlag. Begge steder er man efter hans opfattelse nær ved intuitionen, forstået som den undergrund, hvor alle ideer har deres ophav.