Foregående: Litteratur Næste: Litteratur Op: FAMØS september 1997

Side 9 sætningen:
Næsten kommuterende matricer

Mikael Rørdam

En lille forhistorie

I kvantemekanikken beskrives den atomare verden ved observable, som typisk ikke kommuterer med hinanden. Mest kendt er måske beskrivelsen af positionen og impulsen af en partikel ved operatorerne

hvor er et element i Hilbertrummet . Faktisk er P og Q såkaldt ubegrænsede operatorer på dette Hilbertrum, og de er ikke definerede for alle . Både P og Q er dog definerede på det tætte underrum bestående af vilkårligt ofte differentiable funktioner med kompakt støtte. For ser vi at

Denne relation kaldes Heisenberg's usikkerhedsrelation. Den giver også et eksempel på ikke kommuterende operatorer, som på en måde er tæt på at kommutere. Operatoren PQ-QP ses nemlig at være begrænset, og dermed lille i forhold til P og Q, som er ubegrænsede.

Et spørgsmål en matematiker (og måske også en fysiker) kunne stille sig selv, er hvor langt P og Q er fra kommuterende selvadjungerede operatorer. Mere konkret kunne man spørge sig selv om en lille perturbation af P og Q kan give eksakt kommuterende operatorer, i.e. findes der kommuterende selv-adjungerede operatorer og , hvor og begge er begrænsede? Svaret hertil er nej, og P og Q er således langt fra kommuterende selv-adjungerede operatorer. (Det kan dog vises, at hvis H er et uendelig-dimensionalt Hilbertrum, så findes kommuterende selv-adjungerede operatorer og på Hilbertrummet , så og begge er begrænsede.)

Voiculescu og Lin

Lad være algebraen af komplekse n kryds n matricer. Betragt heri matricerne

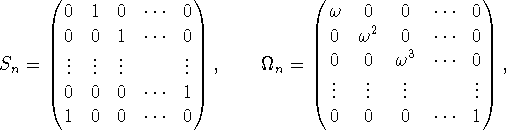
hvor . Det er rutine at eftervise, at matricerne og er unitære, dvs. og tilsvarende for . Endvidere har vi relationen

Kig også på de selv-adjungerede matricer

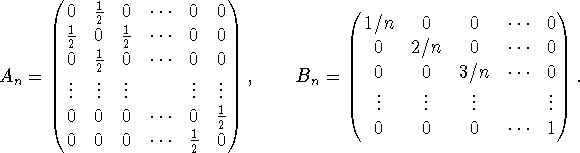
Hvis n er stor, så er tæt på 1 (faktisk er ), og dermed er tæt på . Tilsvarende er tæt på . For at præcisere disse udsagn indføres en metrik på . Den (for operatoralgebraikere) mest naturlige metrik kommer fra operatornormen, som er bestemt ved

hvor angiver den euklidiske norm på .

Det er let at se, at . En udregning viser, at

Kan en sommerfugls vingeslag skubbe til og , hhv. til og , så de kommer til at kommutere? Vi kan formulere dette spørgsmål i mere matematiske termer som følger:

 

 

Nedenstående sætning af Dan Voiculescu (se [4]) viser, at svaret til Spørgsmål 1 er ``nej'':

 

Man kan i øvrigt også udelukke eksistensen af (ikke-nødvendigvis-unitære) kommuterende matricer tæt ved og , se [1]. En kær sætning har mange beviser, og denne er ingen undtagelse. Her kommer en skitse til et elementært bevis for Sætning 3:

Man kan ved at bruge et kompakthedsargument ret let vise:

Denne sætning kan dog ikke bruges til at afgøre spørgsmålene 1 og 2, da udfra et kompakthedsargument ikke kan gøres uafhængigt af n.

Man kan give et ganske avanceret bevis for Voiculescu's sætning, som benytter sig af topologiske egenskaber ved 2-torus .

I , mængden af kontinuerte komplekse funktioner på , har vi to kommuterende unitære funktioner , , j=1,2. Hvis er en matrix algebra, en funktionsalgebra, eller mere generelt en -algebra med 1-element, og hvis er unitære elementer i , så findes netop en *-homomorfi , som opfylder for j=1,2. På denne måde ligger der en 2-torus bag (eller foran) ethvert par af kommuterende unitære elementer (i en matrix algebra, en funktionsalgebra, eller mere generelt i en -algebra). Tilsvarende kan man til et par af næsten kommuterende unitære elementer associere en (lettere deformeret) 2-torus.

Specielt ligger der en 2-torus og spøger bagved Voiculescu matricerne og . Den topologiske obstruktion, vi skal have fat på, udtrykkes mest elegant ved K-teori, eller ækvivalent, ved det faktum, at har et ikke trivielt komplekst liniebundt. Man kan vise, at denne underliggende topologiske obstruktion er bevaret af Voiculescu matricerne, hvorimod obstruktionen for to kommuterende unitære matricer altid er nul. (Omvendt, har man to næsten kommuterende unitære matricer, hvor denne obstruktion er nul, så er de faktisk tæt på to kommuterende unitære matricer.)

Det topologiske rum, som ligger bagved to kommuterende, eller næsten kommuterende, selv-adjungerede elementer af norm 1 er enhedskvadratet . Dette rum er kontraktibelt, i.e. det kan kontinuert deformeres til et punkt, og der er derfor ingen interessante topologiske invarianter knyttet til det. Så måske ligger næsten kommuterende selv-adjungerede matricer tæt på eksakt kommuterende selv-adjungerede matricer?

Der var nok to grunde til, at man tvivlede. For det første fandt man næsten kommuterende selvadjungerede operatorer på et (uendeligt dimensionalt) Hilbertrum, som ikke ligger tæt på kommuterende selv-adjungerede operatorer (dette eksempel er gengivet i [2]). Dernæst er det svært at få øje på kommuterende approximanter til de to næsten kommuterende selv-adjungerede matricer og .

Tvivlerne måtte tvivle om igen, for i 1992 viste Huaxin Lin (i [3]) nedenstående sætning, som specielt implicerer, at svaret på Spørgsmål 2 er ja!

 

Set med en -algebraikers øjne er det glædeligt, at dette yderst konkrete udsagn vises ved at benytte metoder fra abstrakt -algebra-teori. Lad os følge beviset for sætningen et lille stykke på vej.

Antag A og B er selv-adjungerede matricer, og sæt T = A + iB. Da er . Hvis Lin's sætning var falsk, ville der findes , og selv-adjungerede matricer af norm , så , samtidigt med, at der for alle og alle kommuterende selv-adjungerede matricer og i gælder . Sæt . Da vil , men har afstand mindst til de normale elementer i .

Vi indfører -algebraerne:

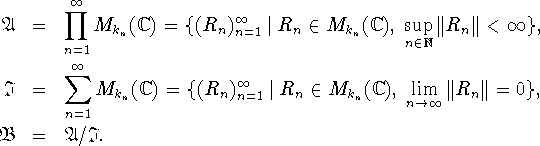
Her er altså et ideal i , og vi har dermed kvotient afbildningen .

Sæt , og bemærk, at er normal, i.e. . Hvis bare vi kunne ``løfte'' til et normalt element , i.e.\ , så er beviset for sætningen halet i land. For da ville alle nødvendigvis være normale, og implicerer , i modstrid med, at ligger ``langt væk'' fra normale matricer.

Man kan ikke almindeligvis i -algebraer løfte normale elementer i en kvotient til normale elementer ``upstairs''. Men den betragtede situation er noget særligt. Lin's ide var at perturbere det normale element en lille smule, så dets spektrum bliver endeligt. (Vi forventer, at spektret for er noget i retning af enhedskvadratet , altså på ingen måde endeligt.) Til brug for denne perturbation blev det helt store krigsmaskineri sat i stilling, og efter en lang og hektisk kamp med meget få overlevende endte Lin med sin ønskede gennemhullede normale operator. Værsgo', næsten kommuterende selv-adjungerede matricer er tæt på kommuterende selv-adjungerede matricer!

Et par år senere havde Peter Friis og jeg den glædelige oplevelse at opdage, at man på meget enkelt vis kan prikke hul i spektret på . Vi observerede følgende:

Vejen fra at have dette ene hul i spektret for til at have det ønskede løft er kort og asfalteret, og beviset for Lin's sætning (Sætning 5) er reduceret til 2-3 sider (se [2]). Det skal understreges, at den bærende ide i beviset fortsat hviler på abstrakt -algebra-teori.

Man kunne afslutte denne historie med et problem: Spørgsmål 2 er blevet besvaret med et ``ja'', så der findes kommuterende selv-adjungerede elementer og i , som approximerer hhv. . Men hvordan ser matricerne og egenligt ud?

Foregående: Litteratur Næste: Litteratur Op: FAMØS september 1997