af Peter Jørgensen
I det sidste nummer af FAMØS før sommerferien stilledes
spørgsmålet: hvilke irrationale tal, x, har den egenskab, at
potenserne,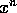 
, nærmer sig heltal, når n vokser? (At en følge,
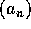, ``nærmer sig heltal'', skal betyde det oplagte: givet
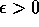skal der findes et N samt heltal, 
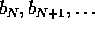, så n > N medfører 
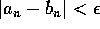). Som
eksempel anførtes 
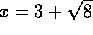, hvis potenser meget hurtigt (fra
og med nr. tre) bliver næsten hele. Næste nummer af bladet rummede et
regnestykke af Bo Markussen, som godtgjorde, at hvis
for et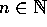 
, har x faktisk den nævnte
egenskab (n=3 giver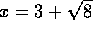 
). Mit mål her er at
vise, hvorledes brug af lidt 3.-års-algebra giver et mere
generelt resultat næsten uden arbejde. Dog skynder
jeg mig at understrege, at jeg kun giver en tilstrækkelig
betingelse på x for, at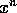 
nærmer sig heltal---det
følgende giver overhovedet intet i retning af at
karakterisere mængden af x'er med denne egenskab.
Først lidt repetition, hvori begreber som gruppe, ring og legeme forudsættes kendte:
På kurset 3AL gennemgås Galois-teorien, som
bla. siger følgende: givet et polynomium,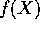 
, med
rationale koefficienter findes et mindste legeme, K, som
indeholder alle rødder til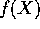 
. Legemet K kaldes
spaltningslegemet for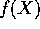 
, og man har 
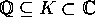. De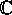 
-dellegemer, der kan opnås
som spaltningslegemer for polynomier med rationale
koefficienter, kaldes normaludvidelser af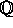 
, evt.\
blot ``normale''. Lad nu K være en normaludvidelse af
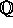. Opfattet som 
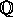-vektorrum har K endelig
dimension, k. Til K knyttes gruppen af K-automorfier:
en K-automorfi,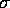 
, er en bijektion, 
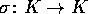, som respekterer plus, gange og
enhedselement (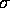
er altså en bijektiv ringhomomorfi
af K ind i K). Hver sådan automorfi fikserer alle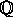 
-elementer, og gruppen af alle automorfier (med
sammensætning som komposition) kaldes K's Galois-gruppe,
og noteres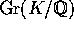 
. Den har netop k
elementer. Endelig: hvis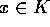 
opfylder 
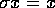for hvert 
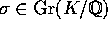, vil faktisk 
.
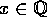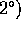Kurset 3AG rummer, udover talrige andre ting,
lidt om algebraiske heltal. Et komplekst tal, x, kaldes et
algebraisk heltal, hvis der findes et polynomium
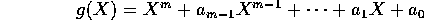
med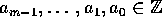 
, hvori x er
rod. Eksempler på algebraiske heltal er alle hele tal, og
mere i almindelighed alle (komplekse) rødder af hele tal
(
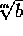er jo rod i 
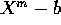). Mængden af
algebraiske heltal noteres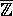 
, og det er en
central ting, at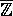 
er en delring af 
.
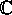Iøvrigt er det let at se, at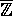 
ikke er et
legeme: hvis nemlig den uforkortelige brøk 
er
et algebraisk heltal, har man
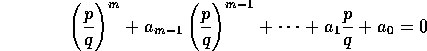
for visse heltal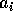 
, og forlænger man med 
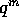og
ordner lidt om, fås
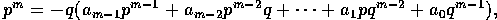
hvilket, da p og q er indbyrdes primiske, kun er muligt dersom q=1. De eneste rationale tal, som også er algebraiske heltal, er dermed de hele tal selv,
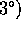Lad K være et 
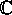-dellegeme, normalt
over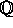 
, og lad 
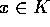. Hvis x er et algebraisk
heltal og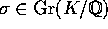 
, er også 
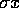et algebraisk heltal: lad nemlig 
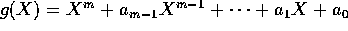være et
heltals-polynomium, hvori x er rod. Så er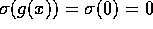 
, men tillige ser man, at
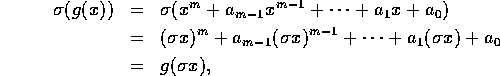
så også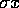 
er rod i 
.
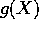Med dette på plads kan man vise
Sætning Lad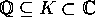 
, hvor
K er en endelig normaludvidelse af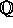 
. Lad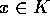 
være et algebraisk heltal. Antag at det for hver automorfi,
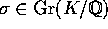, gælder, at enten er 
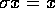, eller også er 
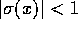. Da vil potenserne,
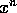, nærme sig heltal, når n vokser.
BEVIS: Man vælger automorfier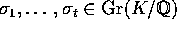 
, så x's forskellige
billeder under automorfierne fra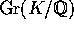 
netop er 
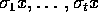. Det kan
antages, at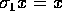 
. Det er klart, at hvis 
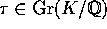er en automorfi, er 
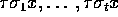igen de
forskellige billeder af x under automorfierne fra
Galois-gruppen, og dermed ses, at hvis n er et naturligt
tal, vil
hvorfor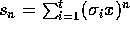 
er
invariant under hele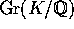 
. Således vil
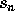iflg. 
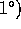ovenfor være et rationalt tal.
Da x er forudsat at være et algebraisk heltal,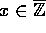 
, vil hvert billede 
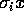iflg.\
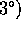ovenfor også ligge i 
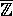, og da
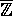iflg.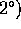 
er en ring, er
åbenbart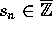 
for hvert n.
Imidlertid ser man nu, at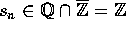 
, jvf. 
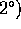ovenfor; det
komplekse tal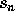 
er faktisk et heltal. Men
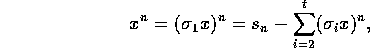
og da 
for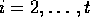 
følger det,
at den sidste sum går mod nul for n gående mod uendelig---
så potenserne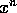 
nærmer sig heltal.
Heraf kan man specielt udlede et resultat, som omfatter
tilfældet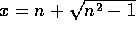 
, nemlig
Korollar Hvis a og d er heltal så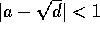 
, vil potenserne 
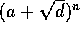nærme sig heltal for
.
BEVIS: Hvis d er et kvadrattal, er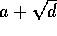 
selv et heltal, og korollarets påstand er triviel. Ellers
sætter man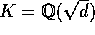 
(dette betegner mængden
af komplekse tal på formen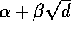 
, hvor
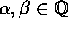). Det er kendt fra 3AL, at
dette faktisk er en normaludvidelse af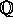 
, hvis eneste
ikke-trivielle automorfi er givet ved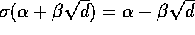 
. Da nu a og
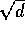er algebraiske heltal, er 
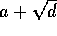et
algebraisk heltal, så forudsætningerne i sætningen ovenfor
er opfyldt, og korollarets påstand følger. 
Imidlertid kan man let få sætningen til at udtale sig om mere komplicerede udtryk---f.eks. har den også som konsekvens, at potenserne af
nærmer sig heltal (her benyttes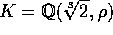 
, hvor 
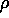er en kompleks tredje enhedsrod).