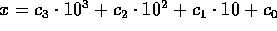 , hvor
, hvor 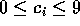 for
for
 og
og 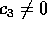 kaldes famøst hvis
kaldes famøst hvis
Desværre havde der indsneget sig nogle grimme trykfejl i opgaven med de Famøse tal. Der skulle naturligvis have stået:
Definition. Et fircifret tal
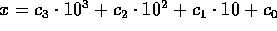 , hvor
, hvor 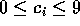 for
for
 og
og 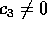 kaldes famøst hvis
kaldes famøst hvis
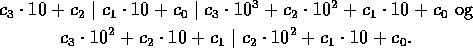
De fire ikke-trivielle famøse tal er 1248, 1664, 1995 og 4998,
der---som den dovne opgavestiller har gjort---kan findes vha. en
computer. Det interessante er imidlertid, at de alle ligger tæt på
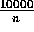 for n=8,6,5,2. Vi har nemlig, at
for n=8,6,5,2. Vi har nemlig, at
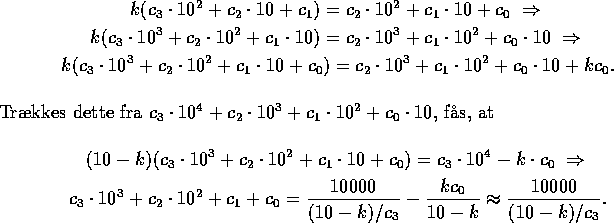
De tre første ikke-trivielle famøse tal har 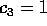 , så
, så
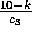 er heltallig, nemlig 8, 6 og 5. Det sidste har
k=2 og
er heltallig, nemlig 8, 6 og 5. Det sidste har
k=2 og 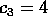 , så
, så 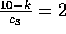 .
.
Det næste tal i følgen 61 52 63 94 46 er 18. Dette kan indses på følgende grimme måde. Tag differencen mellem to tal, der står ved siden af hinanden, to gange:
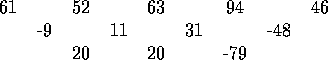
Som det tydeligt fremgår er 46 ``forkert.'' Hvis 20-mønsteret skulle have passet, skulle der have stået 145 -- men det passer jo til gengæld fint: 46 er 145, hvor man har flyttet lidt på 1-tallet. Det næste tal i rækken er således 145 + 71 = 216, det vil sige 18, da vi leger med på legen.
Den pæneste måde at løse opgaven er at ombytte første og andet ciffer. Så fremkommer kvadratfølgen. Heri er næste tal 81, dermed er følgens næste tal 18.
Opgaven gik ud på at finde n, når 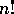 =
10.888.869.450.418.352.160.768.000.000, på den letteste måde: Tallet
ender på 6 nuller, så
=
10.888.869.450.418.352.160.768.000.000, på den letteste måde: Tallet
ender på 6 nuller, så 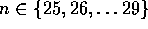 . Ved at
multiplicere tallene fra 1 til 29 og kun beholde det sidste ciffer,
som ikke er et nul, fås at dette tal er 4 for 25!, 26! og 28!, det er
8 for 27! og 6 for 29!. Dermed kan vi slutte at n = 27.
. Ved at
multiplicere tallene fra 1 til 29 og kun beholde det sidste ciffer,
som ikke er et nul, fås at dette tal er 4 for 25!, 26! og 28!, det er
8 for 27! og 6 for 29!. Dermed kan vi slutte at n = 27.
Digitalurs-opgaven: Fænomenet er, at alle cifre viser det samme. Klokken er 22:22.
De irrationale tal: Ja, der findes irrationale tal a,b hvor 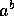 er
rational. Det er ikke klart (i det mindste ikke for mig), om
er
rational. Det er ikke klart (i det mindste ikke for mig), om
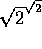 er irrational. Men hvis
er irrational. Men hvis 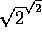 er
rational, vil
er
rational, vil 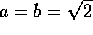 opfylde kravet, hvis ikke, da passer
opfylde kravet, hvis ikke, da passer 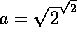 og
og 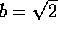 .
.