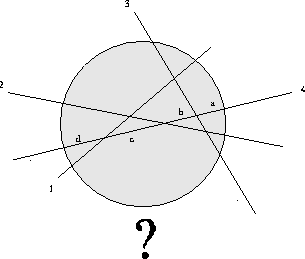
Figure: Hvor mange stykker kan vi højst få, hvis vi snitter en gang til?
Af Martin Jul
Hvor mange stykker pizza kan man højst få, hvis man deler en pizza med n retlinede snit?

Figure: Hvor mange stykker kan vi højst få, hvis vi snitter en gang til?
For at få en fornemmelse af problemet, er det en god idé at betragte
små n. Vi starter med at lægge et snit og ser, at det deler
pizzaen i to stykker. Hvis vi nu vil lægge endnu et snit, kan vi gøre
det på to måder. Enten krydser vi det allerede lagte snit og får
således fire stykker. Eller vi snitter vi parallelt og får kun tre.
Det samme gentages, når vi lægger endnu et snit. Det gælder altså
om at krydse flest mulig af de foregående snit. Resultatet
for  fremgår af tabellen nedenfor.
fremgår af tabellen nedenfor.
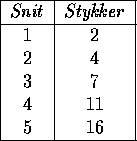
På baggrund af dette gætter vi på, at vi med det n'te snit kan få n nye stykker. Det er nemt at indse, at det altid kan gøres: Da vi har endeligt mange foregående snit, kan vi altid lægge det n'te snit, så det krydser samtlige tidligere snit---vi skal bare lægge det, så det ikke er parallelt med nogle af de foregående. Hvis vi samtidig sørger for, at det ikke går gennem nogle af de tidligere skæringspunkter maksimerer vi også antallet af nye stykker. Det ses let, at vi ved at snitte på denne måde får netop n nye stykker, når vi skærer de n-1 tidligere snit. Bedre kan vi ikke gøre det, da det netop er ved skæring af tidligere snit, at vi skaber nye stykker.
Nu er der kun et problem tilbage: nogle af skæringspunkterne risikerer at ligge uden for pizzaen! Det klares imidlertid nemt ved nedskalering og translation, så skæringspunkterne flyttes til pizzaens indre.
Så langt så godt. Vi ved nu, at vi med n snit kan få  stykker. Formlen er lidt kluntet, så vi vil finde et udtryk for
summen.
stykker. Formlen er lidt kluntet, så vi vil finde et udtryk for
summen.
Det er nemt. Vi betragter to gange summen

hvoraf det følger, at 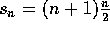 . Det siges, at Gauss indså
dette allerede som 9-årig! I alt har vi altså følgende sætning:
. Det siges, at Gauss indså
dette allerede som 9-årig! I alt har vi altså følgende sætning:
Pizzasætningen. Det maksimale antal
stykker, der kan opnås ved n retlinede snit i en pizza er
 .
.
Vi bemærker, at det eneste, vi implicit har antaget om pizzaens façon er, at den er en konveks delmængde af planen: Var dette ikke tilfældet, ville der findes et snit, der deler et stykke i mere en to.
Der er nu mange spørgsmål der melder sig. Det mest nærliggende er vel: ``Hvor mange stykker får vi ud af en calzone-pizza?'' eller med andre ord, hvad er resultatet, hvis pizzaen er en kugle, hvor vi allerede har foretaget et snit (denne gang snitter vi med planer)? Eller hvad sker der, hvis vi arbejder i en ikke-euklidisk geometri, og således ikke kan garantere, at ikke-parallelle linier skærer hinanden. Spørgsmålene er åbne. Hvis nogen har lyst til at bruge en sval sommeraften med en drink og lidt pizzaproblemløsning trykker vi med fornøjelse resultatet. Vi glæder os til at se de indsendte løsninger, og ønsker læserne en god sommer.