Henrik Chr. Grove
Ved en af de første Mat1 forelæsninger stifter nye russere bekendtskab med de komplekse tal, men det er sikkert de færreste, der tør påstå, at de er rigtigt fortrolige med disse nye ``sære'' tal. Formålet med denne artikel er først og fremmest at vise, at komplekse tal slet ikke er så sære endda og at give et eksempel på et af de (mange) tilfælde, hvor de komplekse tal viser sig at være en mere ``komplet'' mængde af tal.
Udgangspunktet er en gammel FAMØS-opgave (marts 1995):
Findes der irrationale tal a og b, såSvaret er ja, men beviset er indirekte og føres normalt på følgende måde:er rational?
,
da er 
enten irrational, og da er vi færdige, ellers er
rational, og så virker
og 
,
idet vi så får, at
. 
. Som vi snart skal se,
er det ``meget'' lettere at løse opgaven for komplekse tal.
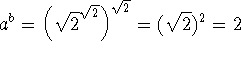Inden vi for alvor begynder at løse opgaven, så lad os med det samme
konstatere, at det ikke er noget problem at finde to imaginære tal z og w
så 
er reel, vi kan nemlig bare vælge z=w=i:
Dette tal kunne være rationalt, og dermed ville vi faktisk have løst opgaven, jeg kender imidlertid ikke noget bevis (eller modbevis) for dette, men hvis tallet skulle være rationalt, ser det ud til at have en meget lang periode i sin decimalbrøksfremstilling. Så vi fortsætter -- og håber, at vi ikke spilder tiden.
Bemærk, at jeg har brugt regnereglen 
, som ikke
bliver gennemgået på Mat 1. Den er dog så let forståelig,
at vi vil bruge den alligevel.
Lad os til at begynde med kun betragte komplekse tal af formen
. Det gør det hele lidt lettere, idet logaritmen til et
komplekst tal af denne form er givet ved: 
.
De første omskrivninger volder ingen besværligheder:
Nævneren i denne brøk er reel, så den vil vi ikke umiddelbart gøre mere ved.
Tælleren er straks noget værre, her bliver vi nødt til at bruge en sætning,
der skyldes Euler, og som siger: 
.
Dette er endnu en sætning, der ikke hører hjemme på Mat1, så endnu en
gang må jeg bede Mat1'erne acceptere en sætning, som dog denne gang gælder
uden forbehold. Hvis vi bruger denne sætning får vi:
Lad os først konstatere, at dette er reelt, hvis bare
thi da er 
, og tallets imaginærdel altså 0. Eftersom de
rationale tal er en delmængde af de reelle, skal denne betingelse altså også
være opfyldt i de tilfælde, vi interesserer os for. Hvis vi i vores udtryk
for 
indsætter, 
, hvor 
, ser vi
let at, tælleren reducerer til 
, og dermed er det kun nævneren,
eller med andre ord m, der bestemmer, om tallet er rationalt. Der er ingen
begrænsninger på, hvilke værdier vi kan vælge for m, thi k er givet ved
som er reelt for alle heltal p, og alle reelle tal m. Ved at kigge lidt på formlen, finder man let på at sætte:
Hermed får vi at 
bliver:
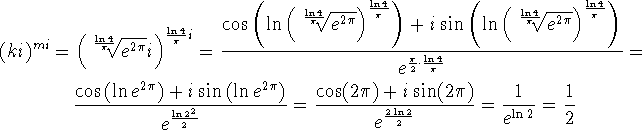
Som det kan ses, fik vi et rationalt tal, som vi gerne ville have, men nu hvor
vi er kommet så langt, er der ingen grund til at glemme det generelle tilfælde
, hvor z og w er vilkårlige komplekse tal. Som før prøver vi bare at
regne løs og ser hvad der sker. Af praktiske grunde præsenterer vi z polært,
og w rektangulært, 
.
Disse omskrivninger burde ikke volde problmer. Den første faktor vil vi nu prøve at bruge De Moivre's formel på, og på anden faktor tager vi den naturlige logaritme, og opløfter e i resultatet, og så får vi:
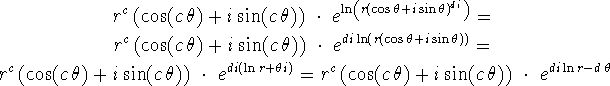
Hvis vi så endnu engang bruger Euler's formel, og flytter lidt rundt, får vi følgende grumt udseende udtryk:
Det er heldigvis ikke så slemt, som det ved første øjekast kan se ud, for hvis man ganger leddene i den store parentes sammen, og bruger additionsformlerne for sinus og cosinus fås følgende udtryk, som er en del ``pænere'':
Igen eliminerer vi først imaginærdelen af resultatet:
Hvis vi indsætter dette i cosinusleddet, ser vi at, dette led ligesom før reducerer
til , hvorfor vi kan konkludere, at hvis
Denne gang kan vi faktisk vælge r, c, d og p frit, idet 
er givet
ved:
Det er selvfølgelig ikke alle valg, der giver et rationalt tal i den sidste
ende, så eftersom vi gerne ville have et rationalt tal, kigger vi på
tallene, tænker os lidt om, og ser, at vi er på den sikre side med at vælge
og p=1. Nu hvor vi besluttede at vælge 
, giver det selvfølgelig
en lille ændring i den ovenstående formel, som bliver til:
Vores to komplekse tal z og w bliver altså
Sluttelig får vi:
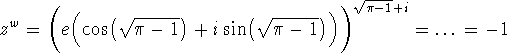
Hvad kan vi så konkludere som afslutning, på alt dette regneri? Vi kan jo starte med at opsummere, hvad vi med sikkerhed har vist.
For det første, har vi fundet rent imaginære tal z og w så
.
For det andet har vi fundet to imaginære tal z og w, med Re 
,
Im , Re 
og Im , så
. Men muligvis kan vi slutte endnu mere,
hverken 
eller 
ser nemlig rationale ud, så måske har vi
fundet komplekse tal i 
, så 
.
Ydermere ser hverken real-, eller imaginærdelen af z, eller realdelen af w
ud til at være rational. Når vi så ser på den utrolig store valgfrihed vi
havde, ser man let, at vi også kunne have valgt d irrational. Vi kan altså
måske finde komplekse tal z og w, der tilhører
, og alligevel få 
,
og sandsynligvis endda også så 
! Med andre ord kan vi
sandsynligvis vælge lige så ``grimme'' komplekse tal z og w, som det skal
være, og alligevel være så heldige, at rammer ned i blandt de
``allerpæneste'' tal.
Under alle omstændigheder, har vi vist, at man blandt de komplekse tal, i
modsætning til blandt de reelle, kan bestemme to tal a og b, så
. Med andre ord kan man sige, at de komplekse tal, er en mere
``komplet'' mængde af tal, end de reelle, simplethen fordi der er så mange, at
vi eksplicit kan pege på to og sige ``de to opfylder det og det krav'', mens
vi nogen gange i de reelle tal, må nøjes med at konstatere, at ``vi kan vise,
at der findes to tal, der opfylder det og det krav, men vi kan ikke pege på
dem''! Eftersom alle reelle tal specielt er komplekse, kan vi ikke komme ud
for det modsatte, men der er sikkert situationer, hvor man heller ikke i de
komplekse tal, kan gøre det bedre end et indirekte bevis.