Foregående: Vi leger med komplekse Op: FAMØS september 1996 Næste: Litteratur

Hvis man blander matematik og fysik kan man få nogle mærkelige resultater. Det er en kendt `skrøne' at fysikerne siger, at summen af de naturlige tal er . har har den fornøjelse at bringe en artiklen af Morten Weis fra Niels Bohr Insitutet, om hvordan man med nogle krumspring, kan opnå dette overraskende resultat. Artiklen lægger hårdt ud, men alle der kan huske lidt kompleks funktionsteori skulle kunne følge argumenterne.

Hvordan fysikerne summerer
de naturlige tal til

Morten Weis
Niels Bohr Institutet
Københavns Universitet

Analytisk udvidelse

Teorien for analytiske funktioner er omfattende, men jeg vil her kort skitsere de vigtigste resultater for hvornår og hvordan analytiske funktioner kan udvides til et større definitionsområde. Materialet i dette afsnit er velkendt og kan f.eks. studeres i [1] [2] [3]. Lad os starte med at repetere Taylors sætning.

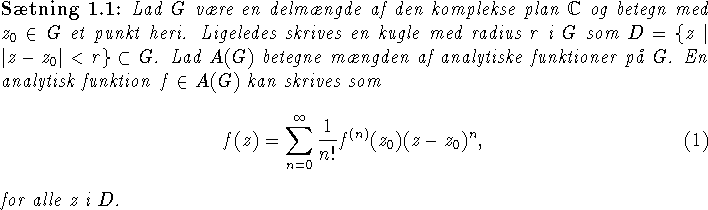
Beviset er velkendt fra f.eks. 2MA [2] og springes over.

Vi vil nu indføre begreber som er nyttige i bestemmelsen af hvornår definitionsmængden for en analytisk funktion kan udvides.

Vi kan erstatte D med enheds-cirkelskiven U.

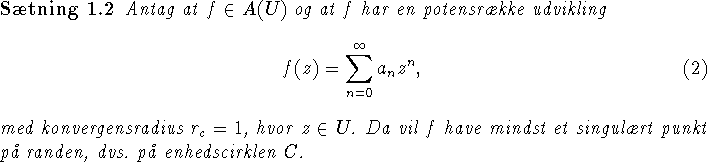
Bevis: Antag det modsatte er tilfældet, så ledes at ethvert punkt i C er et regulært punkt for f. Idet C er kompakt vil der eksistere en endelig følge af kugler , således at centeret af hver kugle ligger på C og at , hvor T er enhedscirklen. Ligeledes må der eksistere funktioner , hvor for alle

Hvis og , så må . Dette skyldes at kuglerne har centrum i C. Deraf vil i . Idet at er sammenhængende vil ifølge korollar 1.1 nedenfor gælde at i . Vi kan derfor nu definere en funktion h på området .

Idet og er en åben mæ ngde, eksisterer der en kugle , hvor . Men idet , og at h i U er givet ved potensrækken for f, som iflg. sætningen nu har konvergensradius , har vi opnået en modstrid med vores antagelser i sætningen.

I beviset benyttes resultatet, kendt som identitetssætningen for analytiske funktioner, der her er gengivet som et korollar.

Bevis: Nulpunktsmængden (defineret i korollar 1.2) Z(f-g) kan ikke bestå af isolerede punkter fra G, derfor må der gælde at Z(f-g)=G.

Her benyttes resultatet fra endnu et korollar.

For bevis, se f.eks. 2MA noterne [2].

Ovenstående resultater kan samles til følgende definition.

Vi vil give definitionen på hvad der menes med en analytisk udvidelse.

Bemærk at vil være entydigt bestemt af og . Beviset for dette bygger på brugen af korollar 1.1 benyttet i et enkelt område efterfulgt af et induktionsargument i antallet af elementer i . Men det er vigtigt at bemærke at udvidelsen afhænger af .

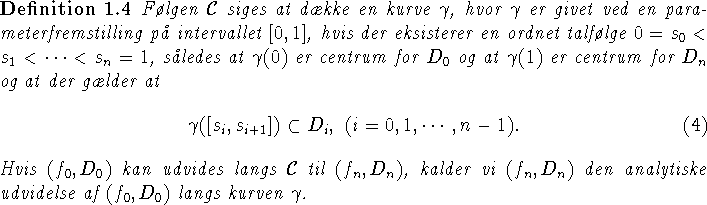
Det vil blive for omfattende at gengive beviset her, men det kan findes i flere lærebøger  [1] [6].

Som vist kan analytiske funktioner udvides til et større område end deres oprindelige definitionsområde, hvis visse betingelser er opfyldt. En analytisk funktion kan udvides til forskellige værdier, dog er den enkelte udvidelse entydigt bestemt. Vi skal nu studere brugen af analytiske udvidelser anvendt på Zetafunktionen.

Riemann's Zetafunktion

Det centrale objekt i denne artikel er Riemanns Zetafunktion, som oprindeligt blev studeret af Riemann til at bestemme antallet af primtal mindre end et bestemt givet tal. Dette vigtige arbejde fra 1859 er genoptrykt på engelsk og kan findes i bogen om Riemanns Zetafunktion af H.M. Edwards [4]. I denne bog er det historiske forløb af studiet af Zetafunktionen gengivet, og jeg vil følge dette samt henvise til mere tidsløse beskrivelser som f.eks. Lang [6].

Den første formel i Riemanns artikel [5] er kendt som Eulers produktformel

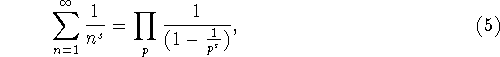
hvor n løber over de hele positive tal og p løber over alle primtal. Dette blev studeret af Dirichlet som beviste Eulers formel for alle reelle værdier af s>1. Derfor kalder vi, som Edwards, venstresiden for Dirichlet funktionen ,

Man mener at Dirichlet opfordrede sin student Riemann til at studere emnet, og det er nu hans navn man forbinder med . Riemann var en af grundlæggerne af den komplekse analyse, så naturligt studerede han problemet for komplekse værdier af parameteren s. Blandt resultaterne han fandt, var at begge sider af Eulers formel er konvergent for , samt at man kan give mening til formlen for alle værdier af s på nær en pol i s=1.

Det er nødvendigt kort at opfriske kenskabet til Gammafunktionen . Det er velkendt at man kan skrive Gammafunktionen i en integral repræsentation, kaldet Mellin transformationer

 

som er en analytisk funktion i den højre halvplan . Grunden til den simple omskrivning er relateret til Mellin transformationsbegrebet, der blot hæfter sig til at dt/t er multiplikativt invariant, så for en absolut integrabel funktion f på intervallet , og for a>0 har vi

Hvis man erstatter t med nt i ligning (7), hvor n er et positivt heltal får man

Riemann foretog nu en sum over n og ved hjælp af resultatet i [8]

kunne han genfinde Dirichlet funktionen

 

På dette sted vender Riemann interessen imod et kurveintegral, med en integrant der ligner formlen ovenfor. Han introducerer

 

hvor kurveintegralet tages fra ind langs den positive reelle akse, rundt om en cirkel omkring nul med radius i positiv omløbsretning, og så tilbage ud til via den positive reelle akse igen. Ligeledes omskrives tæ lleren som

Med den sædvanlige definition af den komplekse logaritme på den åbne delmængde så bliver ikke defineret på den positive relle akse, som nu er et såkaldt cut eller branched point [7]. Det betyder at kurven beskrevet ovenfor er misvisende, idet man skal integrere lige over og under den positive relle akse. Med integrationen i tilstedeværelse af et sådan cut kommer der et fasebidrag til integralet [6]. Vi opsplitter kurven i 3 bidrag

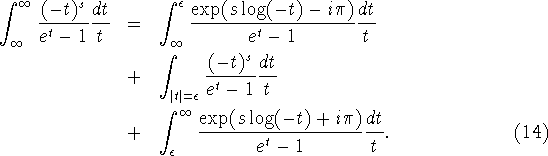
Det kan vises at bidraget fra cirkel integralet forsvinder, når man tager grænsen  [4]. Når denne grænse er taget bliver integralet

 

Indsæt nu ligning (11)

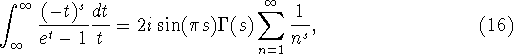
hvis man nu benytter følgende resultat om Gammafunktionen

og endeligt ganger begge sider af lighedstegnet med udtrykket

finder vi Dirichlet funktionen

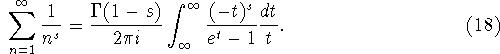
Vi definerer Riemann's Zetafunktion som højresiden af dette udtryk

 

Som nævnt ville Riemann finde en formel gyldig for alle værdier af s, og integralet i ligning (19) er faktisk konvergent for alle værdier af s. Betragtes integranten vil nævneren dominere tælleren fordi vokser hurtigere end uanset værdien af s, når . Ligeledes kan man se at er analytisk overalt, med evt. undtagelse af punkterne hvor Gammafunktionen har simple poler. For værdierne har ingen poler, hvilket betyder at integralet i ligning 19 har nulpunkter, der ophæver polerne af i disse punkter. For s=1 er Dirichlet funktionen divergent og har en simpel pol, idet er en simpel pol. Vi ser, at Riemann's Zetafunktion er analytisk for alle , pånær en simpel pol i s=1. Vi har foretaget en analytisk udvidelse af Dirichlet funktionen til hele den komplekse plan, pånær s=1. Denne udvidelse er som vist i første afsnit entydig bestemt. Når Riemann ikke selv omtaler sit arbejde som en analytisk udvidelse, men som at finde et udtryk for Dirichlet funktionen som er gyldigt for alle s, så\ skyldes det ifølge Edwards [4] at Riemann opfattede holomorfe funktioner som noget man skulle diskutere globalt og ikke lokalt ved potensrækker. Den lokale formulering med potensræ kker, hvor en analytisk udvidelse diskuteres ved familier af kugler, med konvergente potensrækker som illustreret i første afsnit stammer fra Weierstrass, og illustrerer en forskel i grundsyn mellem de to matematikere.

Vi skal nu studere værdierne af Riemanns Zetafunktion for . Funktionen

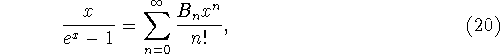
er analytisk omkring x=0 og derfor kan den udvikles i en potensræ kke som skrevet på højresiden, hvor koefficienterne er Bernoullitallene. Lad s=-n for og indsæt i ligning (19)

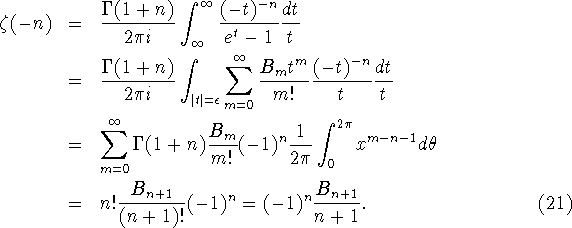
Man kan nu finde værdierne . Da alle er nul vil for alle heltal .

Som den vågne læser nu kan se er her kimen til artiklens titel.

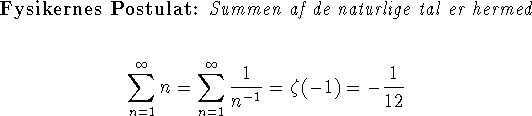
Bevis: Intet - udsagnet er noget vrøvl. Fordi to analytiske funktioner er ens på en åben delmængde af den kompekse plan, og deraf er hinandens analytiske udvidelser til deres respektive definitionsmængder, så kan man ikke sige at deres værdier er ens i disse definitionsmængder. Man kan kun sige at de er entydigt bestemt af hinanden. Riemann's Zetafunktion er ikke lig Dirichlet funktionen for .

Regularisering i feltteori.

I fysik benyttes de såkaldte kvantefeltteorier til at beskrive de fundamentale vekselvirkninger i naturen, som f.eks.\ elektromagnetisme. Disse teorier er karakteriseret ved at indeholde uendelig mange frihedsgrader, dvs. informationer om det fysiske system, nemlig mindst én talværdi knyttet til hvert punkt i rummet. I hvert punkt beskrives en operator hvis forventningsværdi beskriver fysikken som i ordinær kvantemekanik, det specielle er det uendelige antal af operatorer. Man har udviklet teknikker til at behandle sådanne systemer igennem de sidste 60 år, men stadig giver næsten alle fysiske udregninger et uendeligt resultat. Derfor skal de ``bearbejdes'' før meningsfuld information kan hentes fra udregningen.

Der er to skridt i denne bearbejdning, benævnt regularisering og renormalisering. Regularisering knytter sig til en hå ndfuld teknikker hvis formål det er at give kontrol over en udregning, enten ved vold at tvinge regningen til at give et endeligt svar, eller ved at lade sig lede af et princip som man ønsker opfyldt af fysiske grunde. I den første kategori findes gitterregulariseringen, hvor rummet erstattes af et gitter, hvorved alle punkter separeres med en gitterafstand fra deres naboer. En typisk situation hvor uendelige resultater fremkommer er hvis man vil studere produktet af to operatorer i det samme punkt i rummet, hvilket man ikke kan tillægge mening, men ved at separere alle punkter bliver regningen endelig. Svaret af sådanne udregninger vil så afhænge af . Kriteriet for om regulariseringen er lovlig er at udtrykket skal gå imod det klassiske resultat i græ nsen hvor regulatoren . Modsat kan man ønske, at regulariseringen skal overholde de symmetrier, som forekommer i teorien man beskriver, det kan være rum-symmetrier som Lorentz invarians i relativistiske teorier eller såkaldt gauge-symmetrier i gaugeteorier. Disse teorier er invariante under visse Lie grupper, som er bestemt af det fysiske indhold i teorien. F.eks. er elektromagnetisme beskrevet ved en U(1) symmetri. Det vil lede for vidt at beskrive gaugeteorier, men emnet er tæt knyttet til differentialgeometri. En metode kendt som dimensionalregularisering er netop en fremgangsmåde som regulariserer, men opretholder invarians under både rum- og gauge-symmetri. Ofte vil et fysisk udtryk væ re angivet som et integral over et d-dimensionalt rum, hvor integralet er divergent idet integranten ikke falder af hurtigt nok imod uendeligt, i forhold til hvor hurtigt volumet vokser, som angivet ved målet . Et brutalt cut-off, hvor man ændrer integrationsgrænsen fra til et vist tal , vil mindske volumet og gøre integralet mere konvergent. Dette er regularisering af samme grove type som gitterregulariseringen. I dimensionalregularisering benyttes istedet en analytisk udvidelse i dimensionen af integralet . Dette mindsker også volumet og øger konvergensen af integralet. Et typisk integral vil have formen

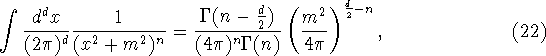
hvor man kan studere kampen mellem integrantens fall-off gennem n og volumets vækst gennem d. Integralet er divergent for n< d/2. Polstrukturen i Gammafunktionen kan studeres, og man kan vise, at i afstanden fra en simpel pol i z=-n finder man

For kort at retfærdiggøre denne diskussion så angiver integralet den simpleste kvantekorrektion til den klassiske beskrivelse af en partikel med masse m, netop hvor en kvantepartikel udsendes med impuls x i et punkt for kort efter at forsvinde i det samme punkt igen. Denne ``kommen og gåen'' i et nu giver et energibidrag til partiklen, og da det kan ske overalt er det ikke underligt, at bidraget bliver uendeligt. Resultatet i den simpleste model af et sådan scenario går som plus led, der ikke er singulære i grænsen hvor . For at kurere denne singularitet kan man på en organiseret måde læ gge et tilsvarende singulært led til med modsat fortegn. Ved at redefinere de parametre, som beskriver teorien man betragter som f.eks. værdien af den elektriske ladning, kan man styre denne udregning til at give den værdi som man må ler i naturen. Man foretager en renormalisation. Vi skal kun benytte regularisering i den følgende diskussion.

På denne måde håber jeg at have illustreret hvordan analytiske udvidelser og renormalisering af uendelige bidrag hører med til fysikkens forunderlige verden.

Kort om Casimir effekten

Der findes et specielt fysisk fænomen kaldet Casimir effekten, opkaldt efter manden som teoretisk forudsagde den, der netop er relevant for Zetafunktionen. Her er det divergente fysiske udtryk relateret til vores diskussion af summen over de naturlige tal. Uden at drage diskussionen for vidt vil jeg kort skitsere hvorledes denne sum optræder i visse fysiske udregninger.

Casimir effekten er relateret til begrebet vakuumenergi eller nulpunktsenergi. Læsere med baggrund i et kvantemekanikkursus vil vide at den harmoniske oscillator (en fjeder der svinger omkring et nulpunkt med en masse m i enden af fjederen) kan kvantiseres, og at man finder uendelig mange diskrete energitilstande mærket ved et kvantetal n der beskriver energiniveauet over systemets grundtilstand

Her er Planks konstant, og er systemets cykliske frekvens, som i det klassiske mekaniske billede er bestemt ved forholdet mellem fjederens ``stivhed'' og massen m. Energien af den kvantiserede fjeder måles nu i enheder (kvanter) af størelse . Allerede i dette simple tilfælde ses det at energien af kvantefjederen i grundtilstanden (n=0) er forskellig fra nul, i modsætning til den klassiske fjeder som ligger helt stille uden nogen energi i grundtilstanden. Så i et kvantesystem som her er der altid en energi knyttet til systemet, selv i den laveste energitilstand.

Kvantefelter kan visualiseres og beskrives som en samling af uendelig mange harmoniske oscillatorer et i hvert punkt af rummet. Hvis teorien er uden vekselvirkninger svinger fjedrene uafhængigt af hinanden, men i en vekselvirkende teori vil svingningerne være koblede. Som en direkte analogi til fjedren i kvantemekanik, vil der være knyttet en nulpunktsenergi til kvantefeltet

hvor summen løber over det uendelige antal ``fjedre'' der beskriver feltet. Normalt ignorerer man nulpunktsenergien, idet den oplagt vil være uendelig. Dette vil vha. Einsteins almene relativitetsteori betyde at universet ville krølles helt sammen idet der vil være en uendelig stor energitæthed i universet. Forestiller man sig nu, at man putter kvantefeltet ind i et afgrænset område af rummet forholder situationen sig nu helt anderledes. Antag at feltet er indespærret mellem to uendeligt store parallelle plader (d-1 dimensionelle hyperplaner) med afstand a mellem sig. Beskrivelsen bliver nu effektivt en-dimensionelt. Der vil stadig være en uendelig nulpunktsenergi, men man kan regularisere det uendelige udtryk. I et specielt simpelt eksempel [9] kan man f.eks. skrive den totale energi som

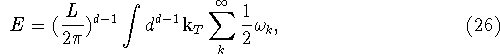
hvor frekvensen er givet ved

hvor n som før er et helt positivt tal, og man med betegner den såkaldte transverse impuls. Man skal forestille sig, at man har puttet hele systemet med felt og plader ind i en stor boks med sidelængde L, hvor . En sådan fremgangsmåde er meget brugt i fysik for at løse problemer vedrørende normalisering, samtidigt kan man argumentere for hvad der sker inde mellem pladerne ikke bør afhænge af noget meget langt væk. Integralet er af samme type som den der blev diskuteret i forrige afsnit og er divergent grundet kampen mellem målet og integranten. Ved dimensionalregularisering findes i m=0 tilfældet (dvs. man betragter et system af masseløse partikler)

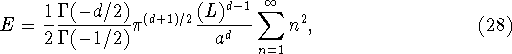
efter integration over impulsen . Her giver den analytiske udvidelse i dimensionen d udtrykket med Gammafunktionen, men der optræder også en divergent sum. Vi kan med baggrund i de forige afsnit lave en analytisk udvidelse som regulariserer summen, og identificere den divergente sum med Riemann's Zetafunktion

Der er ikke nogen markant forskel på at regularisere en divergent sum istedet for et integral. Vi kan nu efter to regulariseringer samt nogle simple omskrivninger bestemme [9]

som er endeligt og negativt for alle positive værdier d. Man kan vise at effekter uden for kaviteten mellem pladerne kancelerer ud og at størrelsen af energien afhænger af geometrien af den kavitet man ønsker. Da energien er negativ vil der udføres et arbejde på pladerne der tiltrækker dem imod hinanden. Denne mystiske effekt kan måles eksperimentielt og siges at give problemer for arbejde i det ydre rum, hvor nulpunktsenergien af det elektromagnetiske felt vil kunne give anledning til ``kold-lodninger'' hvor små hulrum mellem pladerne i et rumskib vil presses sammen af denne kvanteeffekt [10].

Diskussion

Det er selvfølgelig svært at forklare et så stort emne som kvantefeltteori på så kort tid som her, uden at det fremstå r som okkult og nok især som matematisk sjusk/snyd. Selv om mange udregninger i kvantefeltteori er af ren formel karakter, så er det blevet klart gennem de sidste små 10 år, at disse metoder kan give eksakte matematiske resultater, til trods for deres matematiske utilstrækkeligheder. Især i topologi har brugen af kvantefeltteoretiske metoder ledt til ny indsigt i studiet af topologiske invarianter i 2, 3 og 4 dimensioner.

For at komme tilbage til artiklens hovedemne, så er det ikke unaturligt at skrønen om summen af de naturlige tal er opstå et. Først er det ikke så velkendt hvordan der findes forskellige versioner af Zetafunktionen, idet Dirichlet funktionen også\ betegnes som Riemann's Zetafunktion i mange bøger.

Endelig så er fysikere jo et humoristisk folkefærd, med hang til at drille matematikere, så det er nok den væsentligste grund til at skrønen er opstået.

Foregående: Vi leger med komplekse Op: FAMØS september 1996 Næste: Litteratur