
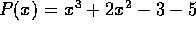 har de tre
rødder a, b og c. Angiv et tredjegradspolynomium med rødderne
har de tre
rødder a, b og c. Angiv et tredjegradspolynomium med rødderne
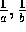 og
og 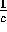 .
.
Jeg vil i dette afsnit forsøge at give et indtryk af, hvor svære opgaverne er i de forskellige konkurrencer. Læseren kan evt. more sig med at (forsøge at) løse opgaverne. Tilladte hjælpemidler er skrive- og tegneredskaber.
Georg Mohr består af 5 opgaver, som skal løses på 4 timer. Opgaverne bygger ikke på kendskab til matematik udover, hvad der kræves på det matematiske gymnasiums obligatoriske niveau. Her er opgavesættet fra dette års konkurrence:

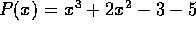 har de tre
rødder a, b og c. Angiv et tredjegradspolynomium med rødderne
har de tre
rødder a, b og c. Angiv et tredjegradspolynomium med rødderne
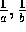 og
og 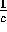 .
.
Som nævnt er sværhedsgraden over det niveau, som findes i gymnasiet. Opgaverne er dog ikke sværere end de fleste af dem kan løses alene ud fra en rimelig solid formalistisk kunnen. Er man lidt bekendt med den slags opgaver, så er de faktisk helt lette (nu er det jo også et par år siden, jeg gik i gymnasiet). Det svære i opgaverne består i, at man selv skal foretage en analyse af problemstillingen (i gymnasiet bliver man jo oftest bare bedt om at gøre dette eller hint). Det er helt bevidst, at opgaverne er så lette, idet Georg Mohr skal være et tilbud til almindeligt dygtige elever. Der stilles dog altid et par svære opgaver, således at de bedste elever kan udskille sig. Nogle af arrangørerne ser gerne, at disse svære opgaver bliver endnu sværere. I den forbindelse vil jeg gerne fremhæve den sidste opgave fra 1991, idet den slet ikke er let, hvis man ikke kender skuffeprincippet:
I den Nordiske Matematikkonkurrence stilles 4 opgaver, som skal regnes på 4 timer. Opgaverne her adskiller sig i sværhedsgrad fra Georg Mohr derved, at de kræver et større kendskab til matematik. Det vil bla. sige kendskab til elementær talteori (specielt restklasseregning), diverse uligheder (i særdeleshed Cauchy-Schwarz) samt diverse klassiske plangeometriske læresætninger, typisk om trekanter, f.eks. Ceva's Sætning---ting, som er blevet nedprioteret i den danske undervisning. Det er således nødvendigt at forberede deltagerne, før de kan deltage i denne konkurrence. Desuden kræver opgaverne mere fantasi og flere gode ideer... døm selv:
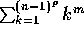 er deleligt med n.
er deleligt med n.
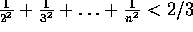 for alle
for alle  .
.
 .
.
 defineret som summen af cifrene i titalsfremstillingen af n.
defineret som summen af cifrene i titalsfremstillingen af n.
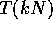 er lige for alle
hele tal k,
er lige for alle
hele tal k, 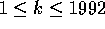 , mens
, mens 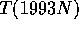 er ulige.
er ulige.
 er lige for alle positive hele tal k.
er lige for alle positive hele tal k.
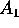 ,
, 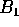 og
og  . Vis,
at
. Vis,
at 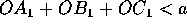 .
.
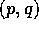 i S gælder, at netop to af punkterne
i S gælder, at netop to af punkterne
 ,
, 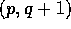 ,
,  og
og 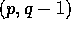 er med i S. For hvilke
værdier af n findes der en to-nabo-mængde med netop n
punkter?
er med i S. For hvilke
værdier af n findes der en to-nabo-mængde med netop n
punkter?
I den Internationale Matematik Olympiade afholdes konkurrencen over to dage, med hver 4.5 timer til 3 opgaver. Opgaver i IMO er svære (læs: rigtig svære). Når man har siddet med dem et stykke tid (dvs. betydelig mere end 4.5 timer), så opdager man til sin overraskelse, at nogle af dem rent faktisk kan løses af almindelige dødelige. Tidspresset gør dog, at alle de sætninger og resultater, som antages kendt, skal sidde på rygmarven, for at man har nogen chance. Udover at man således skal kende temmelig mange resultater om trekanter, talteori, polynomier, uligheder osv., så skal man helst også få en god idé. Opgaverne kan sjældent løses ved, at man bare kører på. De sværeste af opgaverne kræver nærmest guddommelig inspiration. Husk, at det er en gymnasieelev, som skal løse 3 af denne slags opgaver på 4.5 timer (for god ordens skyld må jeg hellere indrømme, at jeg er blevet fristet til at tage mange ``opgave 6'''ere med, som typisk er den sværeste opgave i sættet):
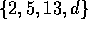 kan finde to
forskellige elementer a og b, således af ab-1 ikke er et
kvadrattal.
kan finde to
forskellige elementer a og b, således af ab-1 ikke er et
kvadrattal.
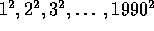 i en eller anden
orden.
i en eller anden
orden.
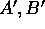 og
og 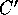 . Bevis, at
. Bevis, at 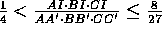 .
.
 af
reelle tal kaldes begrænset, hvis der findes en konstant C, så
af
reelle tal kaldes begrænset, hvis der findes en konstant C, så
 for alle
for alle 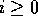 . Der er givet et
vilkårligt reelt tal a>1. Konstruer en begrænset uendelig
følge
. Der er givet et
vilkårligt reelt tal a>1. Konstruer en begrænset uendelig
følge 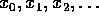 så
så  , for ethvert par af forskellige ikke-negative
hele tal i, j.
, for ethvert par af forskellige ikke-negative
hele tal i, j.
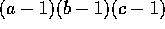 går op i abc-1.
går op i abc-1.
 brikker et kvadratisk net af felter med n horisontale og n vertikale rækker. Et
træk i spillet er, at en brik kan hoppe over et optaget nabofelt til
dettes nabofelt, hvis det ikke er optaget. Samtidig fjernes brikken, som
blev hoppet over. Retningen af hoppene er enten horisontale eller
vertikale. Bestem for hvilke n dette spil kan slutte med én brik
tilbage på brættet.
brikker et kvadratisk net af felter med n horisontale og n vertikale rækker. Et
træk i spillet er, at en brik kan hoppe over et optaget nabofelt til
dettes nabofelt, hvis det ikke er optaget. Samtidig fjernes brikken, som
blev hoppet over. Retningen af hoppene er enten horisontale eller
vertikale. Bestem for hvilke n dette spil kan slutte med én brik
tilbage på brættet.
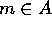 og
og  , som hver er et
produkt af k forskellige elementer fra S for et
, som hver er et
produkt af k forskellige elementer fra S for et 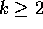 .
.
Jeg har ikke selv deltaget i Baltic Way konkurrencen. Det er dog mit indtryk, at sværhedsgraden er omtrent den samme som i den Nordiske konkurrence. At opgaver løses i fællesskab skal nok tages med lidt forbehold. De 5 deltagere skal på 4 timer løse 20 opgaver. Det betyder, at opgaver ikke løses i en (thedrikkende) rundkreds men uddeligeres til de enkelte deltagere. Samarbejdet består mest i, at deltagerne skal være villige til at slippe en opgave til en af deres medløsere, hvis de ikke selv kan løse pågældende opgave. Her kommer de første 6 opgaver fra konkurrencen i 1993:
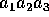 og
og 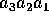 er to tre-cifret decimal tal, med
er to tre-cifret decimal tal, med 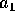 og
og  forskellige tal, som ikke er nul. Kvadrater af disse tal er fem-cifret tal
forskellige tal, som ikke er nul. Kvadrater af disse tal er fem-cifret tal  og
og
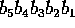 henholdvis. Find alle sådanne tre-cifret tal.
henholdvis. Find alle sådanne tre-cifret tal.
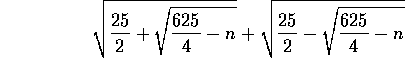
er et heltal.
 delelig med
delelig med  .
.
 og
og 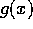 er defineret for alle x, 2 < x < 4, og opfylder
er defineret for alle x, 2 < x < 4, og opfylder
 ,
, 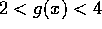 ,
, 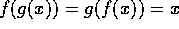 og
og 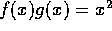 for alle
2 < x < 4. Bevis, at
for alle
2 < x < 4. Bevis, at  .
.
I de sidste afsnit vil jeg beskæftige mig med den elitære del af disse konkurrencer.