Jette Randløv
På rundturen gennem tallene, deres konstruktion,
repræsentation og historie er vi bl.a. stødt på 
og
(= 
). Disse to mængder af tal med
kompositionerne + og 
bruger vi til daglig, fordi de er
legemer. Et naturligt spørgsmål er, om 
på tilsvarende
måde kan gøres til legeme. Svaret er nej - og ja.
For en god ordens skyld starter vi med definitionen på, hvad det vil sige at være et legeme.
Vi siger, at ( 
, 
$) er et legeme, hvis følgende er opfyldt:
og 
og 
har to elementer 
og 
, hvor 
.
findes et inverst (mht. 
-
x 
, så x + - x = 0 
x {0} findes et inverst (mht.
$) element 
, så 
. er neutralt element for 
0 + x = x 
1 er neutralt element for $ altså 
.
kan ikke gøres til et legeme
kan ikke gøres til et legeme, som indeholder
som del-legeme, dvs. et legeme, hvor addition og multiplikation
opfører sig, som de plejer. Beviset for dette er ikke så svært:
Antag er et skæv-legeme, (``skævlegeme'' betyder at den
kommutative lov for multiplikation er opfyldt pånær fortegnet), og at
så 
, og er dellegeme, samt
at
. Der gælder så, at 
giver en modstrid.
Faktisk gælder der at 
eller 
, hvor
betegner kvaternionerne, som vi kommer tilbage til senere.
Det overlades til læseren eventuelt at generalisere nedenstående
bevis.
Da er indeholdt i 
som dellegeme, kan vi uden
videre stryge alle `` 
'', uden at der opstår mulighed
for forvirring.
Vi starter med følgende observation.
Et vilkårligt andengradspolynomium med reelle koefficienter kan
skrives som 
eller som
hvor 
.
Lad f være et polynomium af den sidste type og lad 
. Da f er vilkårlig, kan vi kræve, at f(a) =
0. Derved fåes, at 
. Vi
har altså at for vilkårlig findes
så 
.
Betragt nu 
som basis for , da findes en basis
med 
. Beviset for denne påstand er
følgende: 
(ellers ville 
ikke være en basis). Vælg så
. Nu er 
for ellers ville
. Vi definerer nu 
ved 
, dvs. 
. Der
gælder så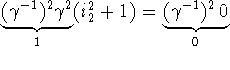 
. Altså
. Påstanden er nu bevist for
. Beviset for 
forløber analogt.
Lad således 
være en sådan basis. Påstanden er nu at
mængden 
er lineært uafhængig. Beviset herfor sker
ved at antage det modsatte, og opskrive en fremstilling af il. 
, hvor 
. Heraf følger 
, eller 
. Der gælder
også, at 
. Derfor må 
. Dette giver
umiddelbart at 
, 
og 
. Men 
, så vi har en modstrid.
Vi har vist, at ikke kan være en basis og at der derfor
ikke kan findes en basis for med de antagelser vi har gjort, og
vi kan konkludere, at ikke kan gøres til et legeme med
som dellegeme.
som legeme
Er man villig til at udelade betingelsen ``med som
dellegeme,'' kan gøres til et legeme - faktisk gør den
følgende fremgangsmåde til et legeme; derfor vil vi i
stedet betragte .
Da har samme kardinalitet som , findes der en
bijektion 
og 
.
$ defineres ved
og
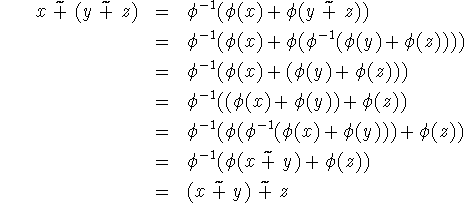
Den associative lov gælder:
Beviset for at den associative lov gælder for multiplikation, indeholder ikke noget nyt. Ligeledes forløber beviset for den den kommutatiove lov og den distributive lov uden overraskelser.
De neutrale elementer defineres mht. addition og multiplkation som
henholdsvis 
og 
. De inverse
defineres som 
og 
. Resten forløber uden overraskelser.
Bemærk forøvrigt, at det intet sted i beviset er brugt afgørende , at
det netop var vi betragtede. Der gælder generelt, at
hvis der findes et legeme med en bestemt kardinatitet, kan alle
mængder med denne kardinalitet gøres til legeme.
Den irske matematiker Sir William Rowan Hamilton (1805-65) brugte i
sidste århundrede en del tid, på at forsøge at gøre til
et legeme med som dellegeme. Af gode grunde lykkedes det
ikke for ham, men han fandt i stedet i 1843 kvaternionerne - 
gjort til et skævlegeme med som dellegeme.
Kvaternionerne er firtupler af reelle tal 
, hvor addition og multiplikation er defineret så 
og i = (0, 1, 0, 0), j = (0, 0, 1, 0) og k = (0, 0, 0, 1)
opfylder 
. Herfra kan udledes, at ij =
-ji = k, jk = -kj = i og ki = -ik = j.
Kvaternionerne har ikke nogle gode egenskaber, som man for alvor
savner hos de komplekse tal, derfor ser man dem sjældent i brug.
Tilgengæld har de en del mindre heldige egenskaber; som nævnt udgør de
ikke et rigtigt legeme, kun et skævlegeme. Endelig gælder algebraens
fundamentalsætning ikke: De fleste n'te grads polynomier har
flere end n rødder. (Eksempelvis, som læseren sikkert
allerede har regnet ud, har 
tre rødder: i, j og k.)
Fra kvaternionerne kan man yderligere fornøje sig med at opbygge Cayley-algebraen, som ikke engang er en ring, da den associative lov for multiplikation ikke er opfyldt.
Der er ikke andre legemer end de komplekse tal, som har
som del-legeme.