Rasmus Borup Hansen
Der er nok få, der bryder sig om at skrive ![]() (se
artiklen om konstruktion af tallene) i stedet for det naturlige tal
fire. Endnu værre er det, hvis man opfatter fire som et reelt tal. Så
skal man (jf. konstruktionen af
(se
artiklen om konstruktion af tallene) i stedet for det naturlige tal
fire. Endnu værre er det, hvis man opfatter fire som et reelt tal. Så
skal man (jf. konstruktionen af ![]() ) angive alle rationale
tal mindre end fire, der hver især er en ækvivalensklasse (jf.
konstruktionen af
) angive alle rationale
tal mindre end fire, der hver især er en ækvivalensklasse (jf.
konstruktionen af ![]() ) af par af ækvivalensklasser (jf.
konstruktionen af
) af par af ækvivalensklasser (jf.
konstruktionen af ![]() ) af mængder, der opfylder de tre
betingelser for at være et naturligt tal. Det er derfor ganske nyttigt
at kunne angive et tal vha. et simpelt system.
) af mængder, der opfylder de tre
betingelser for at være et naturligt tal. Det er derfor ganske nyttigt
at kunne angive et tal vha. et simpelt system.
De fleste af FAMØS's læsere ved vel, at vi i dag hovedsageligt bruger et titals positionssystem (dvs. et positionssystem med grundtal 10) til at repræsentere tal. De fleste ved nok også, at computere og lommeregnere oftest bruger det binære talsystem internt (altså et positionssystem med grundtal 2). Men som vi skal, er dette slet ikke de eneste muligheder.
Med skrivemåden ![]() forstår
vi tallet
forstår
vi tallet
![]()
Vi siger, at ![]() er tallet
a skrevet i et positionstalsystem med grundtal b. I vores
sædvanlige talsystem er b=10 og vi vælger
er tallet
a skrevet i et positionstalsystem med grundtal b. I vores
sædvanlige talsystem er b=10 og vi vælger ![]() 'erne blandt cifrene
0, 1, 2, 3, 4, 5, 6, 7, 8 og 9. I det følgende vil alle tal, der er
skrevet i titalssystemet, blive skrevet
'erne blandt cifrene
0, 1, 2, 3, 4, 5, 6, 7, 8 og 9. I det følgende vil alle tal, der er
skrevet i titalssystemet, blive skrevet ![]() , dvs. uden parenteserne og angivelse
af grundtallet.
, dvs. uden parenteserne og angivelse
af grundtallet.
Sædvanligvis kræves, at ![]() , og at
, og at
![]() , men vi skal se eksempler på, at det ikke
nødvendigvis behøver at være sådan.
, men vi skal se eksempler på, at det ikke
nødvendigvis behøver at være sådan.
Udover titalssystemet kan man også støde på det binære talsystem
(b=2, ![]() ), det oktale talsystem (b=8,
), det oktale talsystem (b=8,
![]() ) og det hexadecimale talsystem (b=16,
) og det hexadecimale talsystem (b=16,
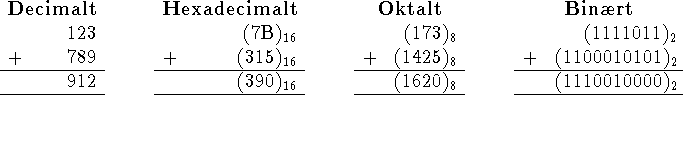 ). Regning i disse talsystemer foregår helt
som i titalssystemet:
). Regning i disse talsystemer foregår helt
som i titalssystemet:
![]()
Det er nemt at se, at der er en simpel sammenhæng mellem tal skrevet
med grundtal b og tal det samme tal skrevet med grundtal ![]() :
:
![]()
hvor
![]()
de to 3-taller i tallene på hexadecimal form i regnestykket ovenfor svarer f.eks. til de to forekomster af 11 helt til venstre i de to nederste linjer i tallene på binær form.
Ofte angiver man, at et tal er negativt vha. tegnet -, men der er
også andre muligheder. Interesserer man sig kun for hele tal, kan man
f.eks. regne modulo ![]() , idet man indskrænker sig til at betragte
tallene
, idet man indskrænker sig til at betragte
tallene ![]() . Hvis
. Hvis ![]() er et ikke-negativt af disse tal, er nemlig
er et ikke-negativt af disse tal, er nemlig ![]() , så
hvis b=n=10 er f.eks.
, så
hvis b=n=10 er f.eks. ![]() .
Tilsvarende bliver
.
Tilsvarende bliver
![]() ,
heldigvis. Den illustrerede metode kaldes ti-komplementnotation.
Ulemperne ved denne metode er, at man må begrænse sig til en endelig
delmængde af de hele tal, at denne mængde ikke er symmetrisk, og at
division med b ikke længere kan foregå blot ved at rykke alle
cifrene en plads til højre.
,
heldigvis. Den illustrerede metode kaldes ti-komplementnotation.
Ulemperne ved denne metode er, at man må begrænse sig til en endelig
delmængde af de hele tal, at denne mængde ikke er symmetrisk, og at
division med b ikke længere kan foregå blot ved at rykke alle
cifrene en plads til højre.
To-komplementnotation bruges flittigt af computere, idet b=2 og
n=32 muliggør repræsentation af tal fra ![]() til
til
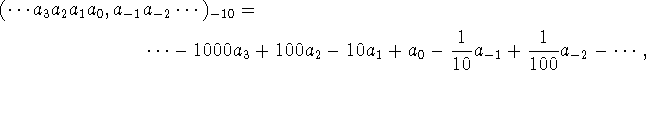 , hvilket er rigeligt til de fleste gøremål.
, hvilket er rigeligt til de fleste gøremål.
En sjældent brugt mulighed for at angive negative tal er at bruge et negativt grundtal. Hvis b=-10, er
![]()
hvor 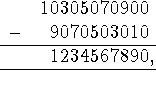 som sædvanlig. Da
som sædvanlig. Da
![]()
må ``negadecimal''-repræsentationen af 1234567890 være
![]() (tag cifrene fra de ulige pladser i 10305070900
og de lige pladser i 9070503010). Tilsvarende fås, da 806040200 -
2040608090 = -1234567890, at
(tag cifrene fra de ulige pladser i 10305070900
og de lige pladser i 9070503010). Tilsvarende fås, da 806040200 -
2040608090 = -1234567890, at 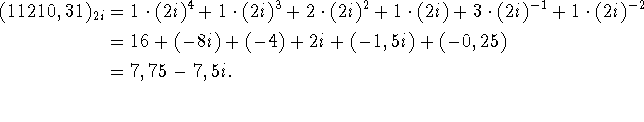 .
Faktisk gælder der [1], at ethvert reelt tal kan
repræsenteres i ``negadecimaltalsystemet'' uden fortegn!
.
Faktisk gælder der [1], at ethvert reelt tal kan
repræsenteres i ``negadecimaltalsystemet'' uden fortegn!
Der er sandelig ingen grund til at begrænse sig til hele endsige reelle grundtal. F.eks. giver grundtallet 2i anledning til det såkaldte ``kvart-imaginære'' talsystem, der har den egenskab, at alle komplekse tal kan repræsenteres vha. cifrene 0, 1, 2 og 3 uden fortegn! F.eks. er
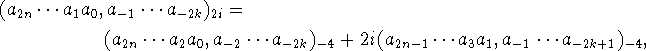
Der gælder endvidere, at
![]()
så konvertering til og fra kvart-imaginær notation reducerer til konvertering til og fra negativ kvartær (grundtal -4) notation. En af fordelene ved kvart-imaginær notation er, at multiplikation og division kan foretages uden at skulle skelne mellem reel- og imaginærdelene, se f.eks. [1].
Endnu en sjov måde at repræsentere tal på er det balancerede trinære
talsystem, der tager udgangspunkt i det trinære (grundtal 3)
talsystem, men i stedet for 0, 1 og 2 bruger 0 og +1 og -1 (i det
følgende skrevet hhv. ![]() ,
, ![]() og
og ![]() ). F.eks. er
). F.eks. er
![]() og
og
![]() .
Det balancerede trinære talsystem
har flere gode egenskaber:
.
Det balancerede trinære talsystem
har flere gode egenskaber:
22220 22021 22102 20221 20002 20100 21202 21000 21101 02221 02002 02100 00202 00000 00101 01200 01001 01112 12202 12000 12101 10200 10001 10112 11201 11012 11110
Som et kuriosum kan nævnes, at den russiske eksperimental-computer SETUN var baseret på det balancerede trinære talssystem. Det kan være, at vi pga. symmetrien og den simple aritmetik en dag vil se flere computere baseret herpå.
Vi bør også kaste et blik på talsystemer med blandet grundtal. Givet
en følge af tal 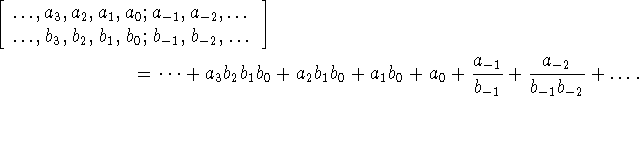 forskellige
fra nul definerer vi:
forskellige
fra nul definerer vi:
![]()
Hvor fjendtligt et sådant talsystem end ser ud, er det faktisk noget, vi kender ret godt fra dagligdagen. F.eks. er 3 uger, 2 dage, 9 timer, 22 minutter, 57 sekunder og 492 millisekunder lig
![]()
Det er muligt at addere og subtrahere tal med blandede grundtal vha. de sædvanlige metoder. Multiplikation og division kræver imidlertid lidt omtanke.
Der er ikke mange, der anvender sædvanlige positionssystemer til at
angive meget store eller små tal, idet det simpelthen er for
upraktisk. Man anvender andre metoder, og f.eks. angives Avogadros
tal ofte som ![]() i stedet for den uoverskuelige
repræsentation i titalssystemet. I det følgende vil sådanne
repræsentationer blive diskuteret.
i stedet for den uoverskuelige
repræsentation i titalssystemet. I det følgende vil sådanne
repræsentationer blive diskuteret.
Ved et flydende tal med grundtal b forstår vi et par af tal (e,f)
med |f|<1 og ![]() , hvor (e,f) repræsenterer tallet
, hvor (e,f) repræsenterer tallet
![]() . Da man sjældent vil angive meget store eller meget små
tal med maksimal nøjagtighed, angiver man ofte kun de p mest
betydende cifre af f, svarende til cifrene lige til højre for
kommaet i en repræsentation af f i et positionssystem, hvor der er
anvendt samme grundtal som i det flydende tal. Der gælder altså, at
. Da man sjældent vil angive meget store eller meget små
tal med maksimal nøjagtighed, angiver man ofte kun de p mest
betydende cifre af f, svarende til cifrene lige til højre for
kommaet i en repræsentation af f i et positionssystem, hvor der er
anvendt samme grundtal som i det flydende tal. Der gælder altså, at
![]() er et heltal, og
er et heltal, og ![]() . Hvis p=6 og b=10
repræsenteres
. Hvis p=6 og b=10
repræsenteres![]() Avogadros tal således af (0.602252,24), og der
gælder, at
Avogadros tal således af (0.602252,24), og der
gælder, at ![]() er et heltal. Sædvanligvis vil
man skrive
er et heltal. Sædvanligvis vil
man skrive ![]() , men i teorien for flydende tal er
det praktisk at ræssonere vha. par.
, men i teorien for flydende tal er
det praktisk at ræssonere vha. par.
Når flydende tal anvendes i computere er b=2, og man begrænser sig til tal, hvor e kan skrives vha. q cifre i et tokomplementsystem. Endvidere bruges en cifferplads til at angive, om f er negativ.
Hvis ![]() og
og 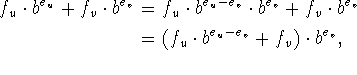 er flydende tal, beregnes summen
u+v ud fra formlen
er flydende tal, beregnes summen
u+v ud fra formlen
![]()
idet ![]() kan udregnes blot ved at flytte kommaet i
kan udregnes blot ved at flytte kommaet i
![]() . Det er her værd at bemærke, at
. Det er her værd at bemærke, at ![]() kan
være større end 1, hvilket der kan rådes bod på, blot ved at flytte på
kommaet og korrigere eksponenten tilsvarende. Multiplikation og
division foregår efter samme principper.
kan
være større end 1, hvilket der kan rådes bod på, blot ved at flytte på
kommaet og korrigere eksponenten tilsvarende. Multiplikation og
division foregår efter samme principper.
Med flydende tal kan man angive en ``passende stor'' delmængde af de
reelle tal vha. forholdsvis få symboler, selvom man lægger bånd på
antallet af cifre i e og f. Hvis vi lader det reelle tal x
repræsenteres af det flydende tal ![]() , bruger man størrelsen
, bruger man størrelsen
![]() som mål for den fejl, man begår. Denne
størrelse kaldes den relative fejl. Multiplikation og division af
flydende tal forstørrer ikke den relative fejl væsentligt. Det gør
derimod addition og subtraktion, hvis man f.eks. vil udregne u+v og
som mål for den fejl, man begår. Denne
størrelse kaldes den relative fejl. Multiplikation og division af
flydende tal forstørrer ikke den relative fejl væsentligt. Det gør
derimod addition og subtraktion, hvis man f.eks. vil udregne u+v og
![]() , eller hvis u-v skal udregnes og
, eller hvis u-v skal udregnes og 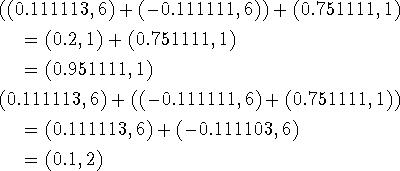 . Faktisk
er det så slemt, at den associative lov ikke gælder for addition af
flydende tal (her er p=6 og q=10):
. Faktisk
er det så slemt, at den associative lov ikke gælder for addition af
flydende tal (her er p=6 og q=10):
![]()
Den associative lov for multiplikation gælder heller ikke, men fejlen
bliver sjældent ret stor. Man kan derimod gå grueligt galt i byen,
hvis man tror, den distributive lov gælder, og heller ikke Cauchys
ulighed får lov til at overleve [1]. De kommutative love for
multiplikation og addition gælder dog stadig. Endvidere gælder, at
hvis u, v og w er flydende tal og ![]() , så er
, så er ![]() og
og ![]() . Hvis endvidere w>0, er
. Hvis endvidere w>0, er ![]() og
og
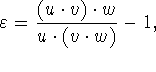 .
.
Selvom regning med flydende tal er unøjagtig, er der en række regneregler for reelle tal, der kan overføres til flydende tal. Endvidere kan man ofte vurdere den relative fejl i de øvrige regneregler så godt nedad, at man ikke behøver bekymre sig om den. Hvis f.eks.
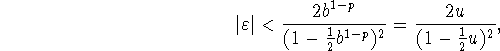
kan man vise [1], at
![]()
hvor ![]() er den mindste værdi, f kan antage.
er den mindste værdi, f kan antage.