Next: Bachelorprojekt---en øjenvidneberetning!
Up: No Title
Previous: EnToTre---førstedelsseminar
af Bo Markussen
Denne sætning var engang med i pensum i en af fortidens
udgaver af 2MA, nedenforstående udgave er således hentet fra Børge
Jessens noter fra 1964--65. Indholdsmæssig og bevisteknisk hører
sætningen egentlig hjemme på 1MA, men man er jo nødt til at vælge, og
man har altså valgt denne udmærkede sætning fra. I dag findes den
implicitte funktions sætningen på Mat 3GE (differential geometri) og
3NA (numerisk analyse), den bruges på Stat 2A (vidergående teoretisk
statistik), og i forbindelse med kurset Selected topics from the
theory of complex functions fandt forelæseren Mikhail Sodin
det besynderligt, at deltagerne ikke kendte denne elementære sætning.
Sætningen udtaler sig om det tilfælde hvor en funktion 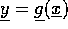 er
givet implicit ved ligningen
er
givet implicit ved ligningen  . Hvis ligningen har
kontinuerte partielle afledede af orden n, og vi kender én
``passende'' løsning
. Hvis ligningen har
kontinuerte partielle afledede af orden n, og vi kender én
``passende'' løsning  , så giver den implicitte
funktionssætning, at
, så giver den implicitte
funktionssætning, at 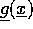 har kontinuert partielle afledede af orden
n samt en ``formel'' for værdien af disse i punktet
har kontinuert partielle afledede af orden
n samt en ``formel'' for værdien af disse i punktet  . Dette kan
bl.a. være nyttigt, hvis vi ikke kan finde løsningsfunktionen
. Dette kan
bl.a. være nyttigt, hvis vi ikke kan finde løsningsfunktionen
 eksplicit. Vi skal da bare finde en enkelt løsning, hvorefter
vi kan approksimere løsningsfunktionen med en endelig Taylorrække. Det
er derfor med fornøjelse, at vi præsenterer...
eksplicit. Vi skal da bare finde en enkelt løsning, hvorefter
vi kan approksimere løsningsfunktionen med en endelig Taylorrække. Det
er derfor med fornøjelse, at vi præsenterer...
Den Implicitte funktionssætning. Lad A være en åben mængde
i 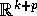 , og lad
, og lad  være kontinuerte funktioner i A med
kontinuerte partielle afledede efter
være kontinuerte funktioner i A med
kontinuerte partielle afledede efter  . Vi sætter
. Vi sætter
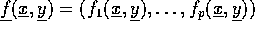 , og betragter
løsningsmængden
, og betragter
løsningsmængden 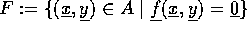 for ligningen
for ligningen  . Lad
. Lad  være en løsning
for hvilken matricen
være en løsning
for hvilken matricen

er invertibel, dvs. 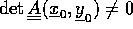 . Og lad
. Og lad  være en åben omegn af
være en åben omegn af
 , hvori
, hvori 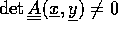 [En
sådan må findes, da
[En
sådan må findes, da 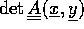 er
kontinuert]. Da eksisterer omegne
er
kontinuert]. Da eksisterer omegne  og
og  af
af  og
og  samt kontinuerte
funktioner
samt kontinuerte
funktioner  i
i 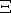 , således at
, således at  afbilder
afbilder 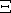 ind i
ind i 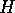 , og
således at
, og
således at 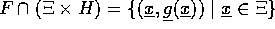 . Forudsættes yderligere, at funktionerne
. Forudsættes yderligere, at funktionerne
 i A har kontinuerte partielle afledede også efter
i A har kontinuerte partielle afledede også efter
 , så vil
, så vil 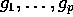 i
i 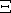 have kontinuert
partielle afledede efter
have kontinuert
partielle afledede efter  . Har funktionerne
. Har funktionerne
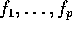 kontinuert partielle afledede af orden
kontinuert partielle afledede af orden 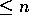 efter
efter
 , vil
, vil 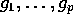 have kontinuert
partielle afledede af orden
have kontinuert
partielle afledede af orden  efter
efter 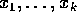 . De
afledede af
. De
afledede af 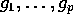 efter
efter  bestemmes i givet
fald ved implicit differention. Dvs. man differentierer ligningerne
bestemmes i givet
fald ved implicit differention. Dvs. man differentierer ligningerne

og løser de fremkomne ligninger.
Beviset er temmeligt besværligt, men uden overraskelser. Det er et af
den slags beviser, som man egentlig godt kan undvære at se, og som
sjældent bliver gennemgået (en tilsvarende skæbne har beviset for den
hyppigt anvendte og citerede transformationssætning fra
integralregningen fået). Også jeg vil derfor nøjes med henvisninger:
Beviset kan findes i W. Rudin, Principles of Mathematical
Analysis, McGraw-Hill, i Børge Jessens gamle 2MA-noter i
A.F. Andersen & H. Bohr, Matematisk Analyse (Bog III). Hvis
læseren selv skulle få lyst til prøve, så kan det anbefales at
betragte tilfældet p=1.
I stedet for vil vi prøve at anvende den implicitte
funktionssætning : Betragt tilfældet, hvor
: Betragt tilfældet, hvor  er givet implicit som
funktion af
er givet implicit som
funktion af  og
og  ved ligningen
ved ligningen
 (vi har altså k=2, p=1).
Det ses, at ligningen tilfredsstilles af punktet
(vi har altså k=2, p=1).
Det ses, at ligningen tilfredsstilles af punktet 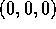 . Idet f
har kontinuerte partielle afledede af vilkårelig høj orden, og
. Idet f
har kontinuerte partielle afledede af vilkårelig høj orden, og
 i punktet
i punktet  , bestemmer
ligningen, idet vi indskrænker os til et at betragte et lille
akseparallelt parallelepipedum omkring dette punkt,
, bestemmer
ligningen, idet vi indskrænker os til et at betragte et lille
akseparallelt parallelepipedum omkring dette punkt, 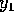 som en
vilkårelig ofte differentiabel funktion g af
som en
vilkårelig ofte differentiabel funktion g af  og
og  .
.
Vi vil finde de partielle differentialkvotienter vha. implicit
differentiation. Vi differentierer altså  mht.
mht.
 og
og  , og sætter lig 0:
, og sætter lig 0:
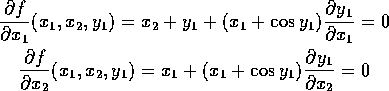
Dermed fås specielt 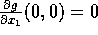 og
og  . Vi vil også finde de partielle afledede af 2.\
orden. Altså differentieres implicit til 2. orden...
. Vi vil også finde de partielle afledede af 2.\
orden. Altså differentieres implicit til 2. orden...

Indsættes 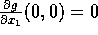 og
og  fås dermed
fås dermed 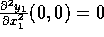 ,
,  og
og  .
Det approximerende
.
Det approximerende  grads polynomium efter Taylors
grænseformel er dermed
grads polynomium efter Taylors
grænseformel er dermed 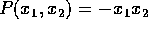



Next: Bachelorprojekt---en øjenvidneberetning!
Up: No Title
Previous: EnToTre---førstedelsseminar
Rasmus Borup Hansen
Mon Mar 6 16:51:54 GMT+0100 1995
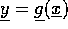 er
givet implicit ved ligningen
er
givet implicit ved ligningen  . Hvis ligningen har
kontinuerte partielle afledede af orden n, og vi kender én
``passende'' løsning
. Hvis ligningen har
kontinuerte partielle afledede af orden n, og vi kender én
``passende'' løsning  , så giver den implicitte
funktionssætning, at
, så giver den implicitte
funktionssætning, at 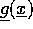 har kontinuert partielle afledede af orden
n samt en ``formel'' for værdien af disse i punktet
har kontinuert partielle afledede af orden
n samt en ``formel'' for værdien af disse i punktet  . Dette kan
bl.a. være nyttigt, hvis vi ikke kan finde løsningsfunktionen
. Dette kan
bl.a. være nyttigt, hvis vi ikke kan finde løsningsfunktionen
 eksplicit. Vi skal da bare finde en enkelt løsning, hvorefter
vi kan approksimere løsningsfunktionen med en endelig Taylorrække. Det
er derfor med fornøjelse, at vi præsenterer...
eksplicit. Vi skal da bare finde en enkelt løsning, hvorefter
vi kan approksimere løsningsfunktionen med en endelig Taylorrække. Det
er derfor med fornøjelse, at vi præsenterer...
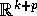 , og lad
, og lad  være kontinuerte funktioner i A med
kontinuerte partielle afledede efter
være kontinuerte funktioner i A med
kontinuerte partielle afledede efter  . Vi sætter
. Vi sætter
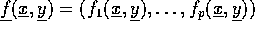 , og betragter
løsningsmængden
, og betragter
løsningsmængden 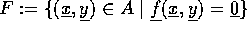 for ligningen
for ligningen  . Lad
. Lad  være en løsning
for hvilken matricen
være en løsning
for hvilken matricen

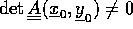 . Og lad
. Og lad  være en åben omegn af
være en åben omegn af
 , hvori
, hvori 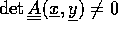 [En
sådan må findes, da
[En
sådan må findes, da 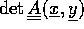 er
kontinuert]. Da eksisterer omegne
er
kontinuert]. Da eksisterer omegne  og
og  af
af  og
og  samt kontinuerte
funktioner
samt kontinuerte
funktioner  i
i 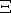 , således at
, således at  afbilder
afbilder 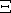 ind i
ind i 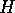 , og
således at
, og
således at 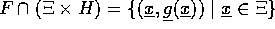 . Forudsættes yderligere, at funktionerne
. Forudsættes yderligere, at funktionerne
 i A har kontinuerte partielle afledede også efter
i A har kontinuerte partielle afledede også efter
 , så vil
, så vil 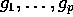 i
i 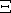 have kontinuert
partielle afledede efter
have kontinuert
partielle afledede efter  . Har funktionerne
. Har funktionerne
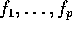 kontinuert partielle afledede af orden
kontinuert partielle afledede af orden 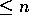 efter
efter
 , vil
, vil 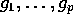 have kontinuert
partielle afledede af orden
have kontinuert
partielle afledede af orden  efter
efter 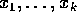 . De
afledede af
. De
afledede af 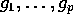 efter
efter  bestemmes i givet
fald ved implicit differention. Dvs. man differentierer ligningerne
bestemmes i givet
fald ved implicit differention. Dvs. man differentierer ligningerne

 er givet implicit som
funktion af
er givet implicit som
funktion af  og
og  ved ligningen
ved ligningen
 (vi har altså k=2, p=1).
Det ses, at ligningen tilfredsstilles af punktet
(vi har altså k=2, p=1).
Det ses, at ligningen tilfredsstilles af punktet 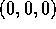 . Idet f
har kontinuerte partielle afledede af vilkårelig høj orden, og
. Idet f
har kontinuerte partielle afledede af vilkårelig høj orden, og
 i punktet
i punktet  , bestemmer
ligningen, idet vi indskrænker os til et at betragte et lille
akseparallelt parallelepipedum omkring dette punkt,
, bestemmer
ligningen, idet vi indskrænker os til et at betragte et lille
akseparallelt parallelepipedum omkring dette punkt, 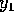 som en
vilkårelig ofte differentiabel funktion g af
som en
vilkårelig ofte differentiabel funktion g af  og
og  .
.
 mht.
mht.
 og
og  , og sætter lig 0:
, og sætter lig 0:
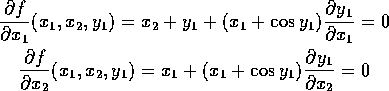
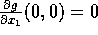 og
og  . Vi vil også finde de partielle afledede af 2.\
orden. Altså differentieres implicit til 2. orden...
. Vi vil også finde de partielle afledede af 2.\
orden. Altså differentieres implicit til 2. orden...

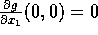 og
og  fås dermed
fås dermed 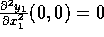 ,
,  og
og  .
Det approximerende
.
Det approximerende  grads polynomium efter Taylors
grænseformel er dermed
grads polynomium efter Taylors
grænseformel er dermed