Sande paradokser i matematik er ikke mulige. Enten kan noget bevises ud fra et konsistent sæt af aksiomer eller også kan det ikke. Sådan er det. Man kan sige, at matematikken er det fag -- det eneste -- som har taget den fulde konsekvens af filosoffernes påstand om, at vi ikke kan vide noget med sikkerhed, på nær måske at vi har en følelse af at eksistere. Hvad vi end tror, vi ved, hviler disse overbevisninger altid på andre overbevisninger. I matematik har man taget følgerne ved at klargøre de grundlæggende overbevisninger, normalt kaldet aksiomer, og forsøgt at minimere antallet. Alt hvad man spørger om er: ``Hvis vi gør disse antagelser, hvad kan vi så slutte?'' Hvorvidt antagelserne er sande, er meningsløst at spørge om.
Ren matematik består udelukkende af påstande, der går ud på at vise, at hvis en vis sætning er sand om noget, så er en vis anden sætning sand om det samme. Det er af vigtighed ikke at diskutere, hvorvidt den første sætning nu virkelig er sand, og ikke at nævne det noget hvorom den antages at gælde. ... Således kan matematik defineres som den videnskab, hvor vi aldrig ved, hvad vi taler om, eller hvorvidt det vi siger, er sandt. Bertrand Russell, [19, p. 360,]
Men helt så enkelt er det alligevel ikke. Der har været nogle
overraskelser i tidens løb. Aksiomssæt, der har vist sig inkonsistente,
sande sætninger, der ikke har kunne bevises, og forestillinger om tallenes
natur som viste sig helt forkerte.
Hvis man kan stille sig tilfreds med at noget ligner et paradoks -- uden at være det: Altså at det ser underligt ud, nærmest selvmodsigende, men ved nærmere eftersyn viser sig ikke at være det -- findes der talrige underholdende eksempler.
Helt simpelt er dette regnestykke:
Fra samme skuffe:
Vi har et afsluttet linjestykke AB. Den ene halvdel, fra A til midtpunktet M, farves gul. Den anden halvdel, fra M til B, farves blå. Nøjagtigt halvdelen af linjestykket er gult og nøjagtigt halvdelen er blåt. Hvilken farve har M?
M kan ikke være gult, for da er netop et punkt mere gult end blåt, og tilsvarende den anden vej. Og M kan selvfølgelig ikke være tofarvet, da punkter pr. definition ikke kan deles.
Matematikken er proppet med interessante tal. Primtallene, perfekte
tal, 
,
e, osv. Mon der blandt de naturlige tal findes uinteressante
tal? 1 er det første tal. 2 og 3 er primtal. 4 er det første
sammensatte tal. 5 er primtal. 6 er perfekt. 7 er primtal. Hvad med
8? Hvis 8 er
uinteressant, må det være det mindste uinteressante tal -- og derfor
interessant! Men så må der findes et andet tal større end 8, som er
det mindste uinteressante tal. På denne måde kan let vises, at der
slet ikke findes uinteressante tal. Martin Gardner førte engang en
lignede argumentation i sin spalte i
Scientific American og modtog et telegram som svar: ``Stop
straks Deres hokuspokus med de uinteressante tal eller lad i hvert fald
for kuriositetens skyld et enkelt blive ved med at
være uinteressant.''
Sætning. Alle heste har samme farve.
Bevis: Ved induktion. For n = 1: I mængder med netop en hest, er det oplagt at alle heste i mængden har samme farve.
Induktionsantagelsen er, at for mængder med n heste har alle heste i mængden samme farve.
Induktionstrinnet: Antag, vi har en mængde med n+1 heste. Fratag en vilkårlig af disse, og betragt de resterende n heste. Det følger af induktionsantagelsen, af disse n heste har samme farve. Betragt igen den oprindelige mængde med n+1 heste og fratag en anden hest. De resterende n heste har ifølge induktionsantagelsen samme farve. Dermed må alle heste i den oprindelige mængde have samme farve.
Det er nu bevist, at alle heste indeholdt i en endelig mængde af heste har samme farve. Q.E.D.
Sætning. For alle 
gælder at a = b.
Bevis: Det er tilstrækkeligt at vise, at for vilkårlige to
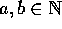gælder, at a = b. Det er ydermere tilstrækkeligt
at vise, at for alle N > 0, medfører 
at a=b. Dette
vises ved induktion efter N:
For k = 1 og 
må for 
gælde at a
= 1 = b.
Induktionstrinnet: Lad 
opfylde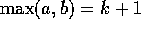 
.
Dermed er 
og det følger af
induktionsantagelsen at a - 1 = b - 1, og dermed a = b.
Q.E.D.
Det overlades til læseren som en opgave, at finde ud af hvad der går galt. Skulle det volde problemer trykker vi gerne løsningen i næste nummer.
Uendelige størrelser har gennem historien givet anledning til megen
panderynken. I dag har vi forstået, hvordan det kan lade sig gøre, at
summen af uendelig mange led, alle strengt større end nul, kan give
noget endeligt, men det forhindrer ikke, at man kan få underlige ting
ud af uendelige rækker. Antag at vi har uendelig mange skuffer og ligeså
mange kugler hver med et naturligt tal påmalet. En af piccoloerne fra
Hilberts Hotel sættes nu til at komme kuglerne ned i skufferne. I
løbet af et halvt minut lægger han den første kugle ned i den første
skuffe. Derefter, i løbet af et kvart minut, tager han den første
kugle op og lægger den ned i skuffe nummer to. I skuffe nummer et
lægges den anden kugle. I det k'te trin bruger han
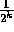-minut på at flytte alle kuglerne fra den skuffe, de
ligger i, til den næste og placere den k'te kugle i den første
skuffe.
Det er klart, at han bliver færdig i løbet af et minut. Alle kuglerne ligger i hver deres skuffe. Hvilken kugle mon ligger i den første skuffe?
I matematikken findes nogle få eksempler på paradokser, som blev opfattet som paradoksale, fordi de stred imod forestillinger, men egentlig ikke mod nogle aksiomer. Cantors paradoks udsiger, at enhver mængde har strengt flere delmængder end den har elementer. Konsekvensen er, at der ikke findes et største kardinaltal. [10] De fleste opfatter næppe dette som paradoksalt i dag. Det er en stor overraskelse, den første gang man hører det -- men ikke paradoksalt.