Next: Paradokser med religiøst
Up: Paradokser i matematik
Previous: Paradokser i matematik
Den naive mængdelæres grundlægger, George Cantor, definerede en mængde
således:
Unter einer `Menge' verstehen wir jede Zusammanfassung M von
bestimmten wohlunterschiedenen Objekten m unsrer Anschauung oder
unseres Denkens (welche die `Elemente' von M genannt werden) zu
einem Ganzen.
Intuitivt set virker det godt nok -- men det er det bare ikke. Det
viste Russell med sit berømte paradoks. Da de fleste læsere velsagtens
kender det til hudløshed, har jeg medtaget det i en knap så kendt
version, nemlig Ota Solgryn formuleringen, bedst kendt fra
1994-udgaven af Mat X.
En Ota Solgryn mængde er en mængde x, som indeholder sig selv som
element:  . Sprogbrugen kommer fra billedet på den gamle Ota
Solgryn-pakke, hvor man ser en dreng komme løbende med en Ota
Solgryn-pakke,
på hvilken man ser en dreng komme løbende med en Ota
Solgryn-pakke,
på hvilken man ser en dreng komme løbende med en Ota
Solgryn-pakke,
på hvilken man ser en dreng komme løbende med en Ota
Solgryn-pakke ...
. Sprogbrugen kommer fra billedet på den gamle Ota
Solgryn-pakke, hvor man ser en dreng komme løbende med en Ota
Solgryn-pakke,
på hvilken man ser en dreng komme løbende med en Ota
Solgryn-pakke,
på hvilken man ser en dreng komme løbende med en Ota
Solgryn-pakke,
på hvilken man ser en dreng komme løbende med en Ota
Solgryn-pakke ...
Betragt nu mængden,  , af alle ikke-Ota-Solgryn-mængder. Altså
, af alle ikke-Ota-Solgryn-mængder. Altså
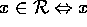 er ikke en Ota Solgryn-mængde,
er ikke en Ota Solgryn-mængde,
med andre ord
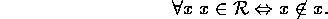
Specielt kan man betragte mængden  . Der gælder så
. Der gælder så

Dette er Russells paradoks.
I ZFC, som i dag er den mest anvendte aksiomatisering af
mængdelæren, forhindres eksistensen af Ota Solgryn mængder af
regularitetsaksiomet:
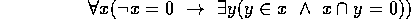
Russell forsøgte selv at løse problemet med typeteorien, der løst sagt går
ud på at inddele de forskellige mængder efter type. Den laveste type
har kun objekter som elementer -- og ikke mængder. Den næste type
indeholder kun objekter og mængder af elementer af den laveste type.
Generelt kan en mængde af en given type kun indeholde objekter eller
mængder af en strengt lavere type.
Hvis en samling af ting ikke overholder disse krav, er det ikke en
mængde. Specielt er Ota Solgryn ``mængden'' ikke en mængde. På denne
måde undgåes Russells paradoks.
I dagligsproget findes analoger til paradokset. Tænk for eksempel på et
bibliotek med to kataloger. Det ene er en fortegnelse over alle de
bøger, som refererer til sig selv, det andet er en fortegnelse over alle
de bøger, som ikke nævner sig selv. I hvilket katalog er det andet
katalog nævnt?
Kurt Grelling opfandt i 1908 det heterologiske paradoks. Han
definerede `heterologisk' til at betyde ord, som ikke beskriver sig
selv. `Ord', `kort', `flerstavelsesord' og `recherché' er alle
ikke-heterologiske, mens `lang', `morgengryfarvet' og `enstavelsesord'
er. Spørgsmålet er, om `heterologisk' er heterologisk?
Russells typeteori fjerner problemerne omkring Russells paradoks, men
ikke omkring disse dagligsprogs-analoger. Det ligger lige for at
forsøge det samme trick med dagligsproget; altså at indføre
hierarkier og forbyde løkker indenfor hierarkierne. I bunden af dette
hierarki er objekt-sproget. Ord herfra må kun referere til ting og
ikke aspekter i objektsproget selv. Det næste lag af hierarkiet,
metasproget, indeholder objektsproget og alle referencer til
objektsproget som kun indeholder ord fra objektsproget. Referencer til
aspekter i metasproget findes så i det næste lag, meta-metasproget.
Ord som `sand' tilhører metasproget, ligeledes gør sætninger af typen
``Denne sætningen er <vilkårligt objektsprogs-ord>''. Men sætninger
som ``Denne sætningen er usand,'' er altså ikke tilladt. Ligeledes er
spørgsmålet ``Er `heterologisk' heterologisk?'' ikke tilladt.
På denne måde får man has på Grellings paradoks og alle paradokser af
Epimenides typen. Til gengæld virker hierarkidelingen kluntet og
u-intuitiv i andre dagligsdags situationer.
Hofstadter skriver [5]:
``In this book, I criticize the theory of types'' would be doubly
forbidden. ... Firstly, it mentions `this book', which should only
be mentionable in a `metabook' -- and secondly, it mentions me
-- a person whom I should not be allowed to speak of at all!
og senere
... the very act of discussing the theory would be the most blatant
possible violation of it!
Det var altså ikke nogen god idé at bruge Russells typeteori som model
for en hierarkistruktur i sproget.



Next: Paradokser med religiøst
Up: Paradokser i matematik
Previous: Paradokser i matematik
Rasmus Borup Hansen
Wed May 31 09:41:45 GMT+0200 1995
 . Sprogbrugen kommer fra billedet på den gamle Ota
Solgryn-pakke, hvor man ser en dreng komme løbende med en Ota
Solgryn-pakke,
på hvilken man ser en dreng komme løbende med en Ota
Solgryn-pakke,
på hvilken man ser en dreng komme løbende med en Ota
Solgryn-pakke,
på hvilken man ser en dreng komme løbende med en Ota
Solgryn-pakke ...
. Sprogbrugen kommer fra billedet på den gamle Ota
Solgryn-pakke, hvor man ser en dreng komme løbende med en Ota
Solgryn-pakke,
på hvilken man ser en dreng komme løbende med en Ota
Solgryn-pakke,
på hvilken man ser en dreng komme løbende med en Ota
Solgryn-pakke,
på hvilken man ser en dreng komme løbende med en Ota
Solgryn-pakke ...
 , af alle ikke-Ota-Solgryn-mængder. Altså
, af alle ikke-Ota-Solgryn-mængder. Altså
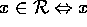 er ikke en Ota Solgryn-mængde,
er ikke en Ota Solgryn-mængde,
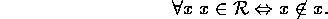
 . Der gælder så
. Der gælder så