


Next: Kursus i LaTeX
Up: No Title
Previous: Leder
Af Jette Randløv
Kaos er et 2-punkters kursus blandt fysik 3 kurserne. Men der
er egentligt intet i vejen for at man kunne tage kurset som
matematiker -- selv uden at have haft noget fysik siden gymnasiet.
Kurset forudsætter et minimum af målteori, som 2MA1 og det nye 3. års
målteori tilfulde dækker. Jeg tror, at matematiske færdigheder i
øvrigt svarende til 2MA1 vil række. Undervisningen består af 2 timers
forelæsninger og 2 timers øvelser om ugen. Lærebogen i år er Edward
Ott ``Chaos in Dynamical Systems,'' Cambridge University Press,
1993, 250 kr. Eksamen er 20 minutters mundtlig bestået/ikke bestået.
Kurset indeholder definition af kaos, kriterier for kaos, kaos i
endimensionale afbildninger, for eksempel afbildningen 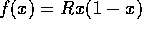 , 0 < R < 4, som -- hvis man ikke allerede var klar over det
-- er overraskende righoldig. Endvidere indeholder kurset i hvert fald
fire forskellige former for fraktale dimensionsbegreber, dynamiske
kendetegn for kaotiske systemer og kaos i Hamilton-systemer.
, 0 < R < 4, som -- hvis man ikke allerede var klar over det
-- er overraskende righoldig. Endvidere indeholder kurset i hvert fald
fire forskellige former for fraktale dimensionsbegreber, dynamiske
kendetegn for kaotiske systemer og kaos i Hamilton-systemer.
Hvis man aldrig har hørt om Hamilton-ligningerne (bedst kendt fra
Analytisk Mekanik), bliver der nok lidt ekstra arbejde med det sidste
emne. Men de nødvendige definitioner og resultater står alle i bogen,
så det skulle ikke være noget problem for en kvik matematiker.
Undervisningen foregår på Niels Bohr Instituttet. De matematikere, som
har hørt om stedet og måske fået en kort rundvisning som et led i
deres almene dannelse, er sikkert begyndt at få nervøse trækninger.
Nuvel -- det er nemt at finde instituttet. Det er simpelthen den
klynge grå og brune bygninger som ligger mellem Riget og
Frimurerlogen. At finde rundt derimod, er en helt, helt anden sag. I
år foregår forelæsningerne i auditorium D. Det nemmeste er at gå
ind igennem ekspeditionen, det vil sige ind, en halv etage ned af
trappen på venstre hånd, ringe på klokken til døren brummer, og til
venstre. Dernæst skal man en halv etage ned af trappen på venstre
hånd, første korridor på venstre, et par trin op, lige frem, en
tredjedel etage op, 360 grader højre-om en etage op ad en hvid og
derefter en smal brun trappe, gennem første dør på venstre hånd, og
man er i auditoriegangen. (Men pas på: Det er den første dør efter den
brune trappe -- og ikke døren efter den hvide trappe. Hvis man tager
den, bliver man slået tilbage til start og må begynde forfra ved
ekspeditionen.) Se, det var jo pærelet. Det er straks meget, meget
værre når man skal finde øvelseslokalet. Kc7 hedder det i år. Og der
er udsigt til Fælledparken. Jeg vil ikke beskrive hvordan man finder
det -- vi forsøger jo trods alt her på Famøs-redaktionen at holde
antallet af sider under de 52. Men man
kan jo altid spørge folk, man møder, om vej. De fleste taler, om ikke
en af-art af dansk, så dog i det mindste en eller anden form for
engelsk.
Men man
kan jo altid spørge folk, man møder, om vej. De fleste taler, om ikke
en af-art af dansk, så dog i det mindste en eller anden form for
engelsk.
Det siges, at instituttet har 4 etager, men 21 niveauer. Jeg tror nu
det er mere; for hvis man går fra øvelseslokalet over til
frokoststuen, hvor det er muligt at trække en varm kakao, som faktisk
er udmærket taget i betragtning, at det er maskinkakao, findes der to
ruter, som er approksimativt lige lange. Går man ad den ene, passerer
man 9 forskellige niveauer, mens den anden fører én forbi 14
forskellige. Og så langt er der heller ikke fra Kc7 til frokoststuen,
man har jo ikke engang været på højde med 4. etage. Derfor formoder
jeg, at der eksisterer strengt mere end 21 forskellige niveauer, og
glæder mig til at nogen vil fremføre et stringent bevis.
En af de mest tekniske detaljer i kaoskurset er nok beviset for
Sarkovskiis teorem. (Findes blandt andet i sidste nummer af
Famøs, side 8, dog uden bevis.) Bevist fylder halvanden side
og er virkelig ikke særlig svært. Generelt er kurset let, hvis man
sammenligner det med niveauet på matematik 3. Men hvis man ikke har de
store forudsætninger og dertil lægger udfordringen i at finde rundt på
NBI -- ja, så er det en helt anden sag.
Jeg synes godt om kurset, blandt andet fordi man får en ordentlig
definition af alle de begreber, man kender fra populære fremstillinger
af kaos-teorier og fra pressen. En del af regneøvelserne hedder noget
i retningen af: ``Skriv et computer program, der beregner og viser de
første 1000 iterationer af...'' Det tager kun et
par minutter, hvis man har et nogenlunde greb om Pascal eller et
lignende værktøj. Til gengæld kan det nemt tage en god time at få
revet sig løs igen, hvis man begynder at manipulere lidt med
ligningerne: Hvad mon der sker, hvis man ganger med sinus i stedet,
farvelægger som funktion af iterationsantallet, inverterer det led
her, tæller antallet af forekomster og afbilder det mod x...?
Nå ja, man kunne jo sikkert spilde tiden med værre ting...
Kaos på NBI. To studerende A og B startes fra samme
udgangstilstand med et lille puf ned ad trappen til NBIs kælder. Efter
kort tid er deres tilstande langt fra hinanden, og de studerende har
ingen hukommelse om deres trajektorie.



Next: Kursus i LaTeX
Up: No Title
Previous: Leder
Rasmus Borup Hansen
Wed May 31 09:41:45 GMT+0200 1995
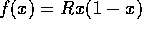 , 0 < R < 4, som -- hvis man ikke allerede var klar over det
-- er overraskende righoldig. Endvidere indeholder kurset i hvert fald
fire forskellige former for fraktale dimensionsbegreber, dynamiske
kendetegn for kaotiske systemer og kaos i Hamilton-systemer.
, 0 < R < 4, som -- hvis man ikke allerede var klar over det
-- er overraskende righoldig. Endvidere indeholder kurset i hvert fald
fire forskellige former for fraktale dimensionsbegreber, dynamiske
kendetegn for kaotiske systemer og kaos i Hamilton-systemer.